题目内容
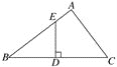
【题目】如图,在![]() 中,
中,![]()
![]() 是斜边
是斜边![]() 上两点,且
上两点,且![]() 将
将![]() 绕点
绕点![]() 顺时针旋转90°后,得到
顺时针旋转90°后,得到![]() 连接
连接![]()
(1)求证: △AED≌△AEF
(2)猜想线段BE,ED,DC之间的关系,并证明
【答案】(1)见解析 (2)![]() ,证明见解析
,证明见解析
【解析】
(1)由旋转的性质可得:AD=AF,∠BAC=∠FAD=90°,由![]() 可得∠FAE=
可得∠FAE=![]() ,所以
,所以![]() ,又AE=AE,故可证△AED≌△AEF
,又AE=AE,故可证△AED≌△AEF
(2)由旋转的性质可得:BF=CD,∠ACB=∠ABF,可证∠FBE=90°,由(1)可得:EF=ED,根据勾股定理可得:![]() ,故可得
,故可得![]()
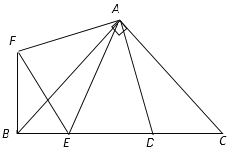
∵△ADC绕点A顺时针旋转90°得△AFB,
∴△ADC≌△AFB,∠FAD=90°,
∴AD=AF,
∵∠DAE=45°,
∴∠FAE=90°-∠DAE=45°,
∴∠DAE=∠FAE,
∵在△AED与△AEF中,
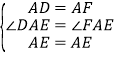
∴△AED≌△AEF(SAS)
(2)∵△AED≌△AEF,
∴ED=FE,∠ACB=∠ABF,
在Rt△ABC中,
∵∠ABC+∠ACB=90°,
∴∠ABC+∠ABF=90°即∠FBE=90°,
∴BE2+BF2=FE2,即BE2+DC2=DE2

练习册系列答案
相关题目