Question

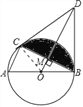
【题目】如图，已知AB为⊙O的直径，BD和CD为⊙O的切线，切点分别为B和C．

（1）求证：AC∥OD；

（2）当BC=BD，且BD=6cm时，求图中阴影部分的面积（结果不取近似值）．

Answer 1

【答案】(1)见解析;(2)( 4π﹣3)cm2．

【解析】分析：（1）连接OC，证明∠OCD=90°．根据切线定理得DC=DB，OB⊥BD，OC⊥CD，证得△OCD≌△OBD，再结合AB为直径，AC⊥BC，可得∠ACO=∠COM，从而得证；
（2）阴影面积=S扇形OBC-S△OBC．根据切线长定理知△BCD为等边三角形，可求∠BOC的度数，运用相关公式计算．

详解：

（1）证明：连接OC．

∵BD和CD为⊙O的切线，

∴DC=DB，OB⊥BD，OC⊥CD，

又OB=OC，

∴△OCD≌△OBD，

∴∠COM=∠BOM，从而易得BC⊥OD，

∵AB为直径，

∴AC⊥BC，

∴∠ACO+∠OCM=∠COM+∠OCM=90°，

∴∠ACO=∠COM，

∴AC∥OD.

（2）∵DB，DC为切线，B，C为切点，

∴DB=DC．

又∵DB=BC=6，∴△BCD为等边三角形．

∴∠BOC=360°﹣90°﹣90°﹣60°=120°，

∠OBM=90°﹣60°=30°，BM=3．

∴OM=，OB=2．

∴S阴影部分=S扇形OBC﹣S△OBC＝