题目内容
【题目】如图,E,F分别是正方形ABCD边AD、BC上的两定点,M是线段EF上的一点,过M的直线与正方形ABCD的边交于点P和点H,且PH=EF,则满足条件的直线PH最多有( )条
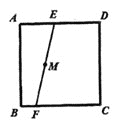
A.1B.2C.3D.4
【答案】C
【解析】
如图1,过点B作BG∥EF,过点C作CN∥PH,利用正方形的性质,可证得AB∥CD,AD∥BC,∠A=∠NBC=90°,AB=BC,再证明BG=CN,利用HL证明Rt△ABG≌Rt△CBN,根据全等三角形的对应角相等,可知∠ABG=∠BCN,然后证明PH⊥EF即可,因此过点M作EF的垂线满足的有一条直线;图2中还有2条,即可得出答案.
解:如图1,过点B作BG∥EF,过点C作CN∥PH,
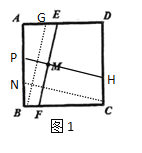
∵正方形ABCD,
∴AB∥CD,AD∥BC,∠A=∠NBC=90°,AB=BC,
∴四边形BGEF,四边形PNCH是平行四边形,
EF=BG,PH=CN,
∵PH=EF,
∴BG=CN,
在Rt△ABG和Rt△CBN中,
![]()
∴Rt△ABG≌Rt△CBN(HL)
∴∠ABG=∠BCN,
∵∠ABG+∠GBC=90°
∴∠BCN+∠GBC=90°,
∴BG⊥CN,
∴PH⊥EF,
∴过点M作EF的垂线满足的有一条直线;
如图2

图2中有两条P1H1,P2H2,
所以满足条件的直线PH最多有3条,
故答案为:C

练习册系列答案
相关题目