题目内容
【题目】已知四边形 ABCD ,有以下四个条件:① AB ∥ CD ;② BC ∥ AD ;③ AB CD ;④ABC ADC .从这四个条件中任选两个,能使四边形 ABCD 成为平行四边形的选法有( )
A.3 种B.4 种C.5 种D.6 种
【答案】B
【解析】
从四个条件中任选两个,共有以下6种组合:①②、①③、①④、②③、②④、③④,然后按照平行四边形的判定方法逐一判断即可.
解:从四个条件中任选两个,共有以下6种组合:①②、①③、①④、②③、②④、③④;
具备①②时,四边形ABCD满足两组对边分别平行,是平行四边形;
具备①③时,四边形ABCD满足一组对边平行且相等,是平行四边形;
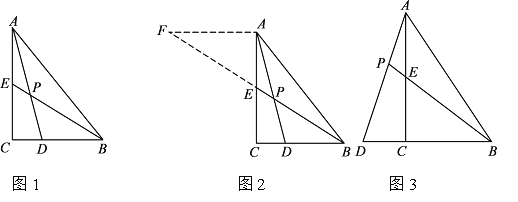
具备①④时,如图,∵AB ∥ CD ,∴ABC +C=180°.
∵ABC ADC,∴ADC +C=180°.
∴AD∥CB .
所以四边形 ABCD 是平行四边形;
具备②③时,等腰梯形就符合一组对边平行,另一组对边相等,但它不是平行四边形,故具备②③时,不能判断是否是平行四边形;
具备②④时,类似于上述①④,可以证明四边形 ABCD 是平行四边形;
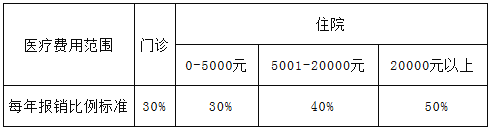
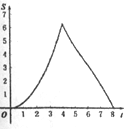
具备③④时,如图,四边形ABCD为平行四边形,连接AC,作AE垂直BC于E;
在EB上截取EC'=EC,连接AC',则△AEC'≌△AEC,AC'=AC.
把△ACD绕点A顺时针旋转∠CAC'的度数,则AC与AC'重合.
显然四边形ABC'D' 满足:AB=CD=C'D';∠B=∠D=∠D',而四边形ABC'D'并不是平行四边形.
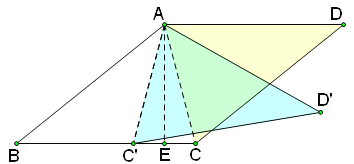
综上,从四个条件中任选两个,能使四边形 ABCD 成为平行四边形的选法共有4种.
故选B.

练习册系列答案
相关题目