题目内容
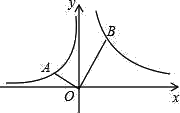
【题目】如图,在某海上观测点B处观测到位于北偏东30°方向有一艘救船A,搜救船A最大航速50海里/时,AB=52![]() 海里,在位于观测点B的正东方向,搜救船A的东南方向有一失事渔船C,由于当天正值东南风,失事渔船C以2海里/时的速度向西北方向漂移,若不考虑大风对搜救船A的航线和航速的影响,求失事渔船获救的最快时间.
海里,在位于观测点B的正东方向,搜救船A的东南方向有一失事渔船C,由于当天正值东南风,失事渔船C以2海里/时的速度向西北方向漂移,若不考虑大风对搜救船A的航线和航速的影响,求失事渔船获救的最快时间.
【答案】失事渔船获救的最快时间为3小时.
【解析】
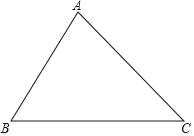
作AD⊥BC于点D,在直角三角形ABD中,根据三角函数求得AD的长;再在直角三角形ACD中,根据三角函数求得AC的长;先求出BC的长,再根据搜救船行驶路程+失事船只漂移路程=AC的长列方程求解可得.
过点A作AD⊥BC于点D,

在Rt△ABD中,∵AB=52![]() 、∠B=60°,
、∠B=60°,
∴AD=ABsinB=52![]() ,
,
在Rt△ADC中,AD=78![]() ,∠C=45°,
,∠C=45°,
∴AC=![]() AD=156,
AD=156,
设失事渔船获救的最快时间为t,
根据题意,得:2t+50t=156,
∴t=3,
答:失事渔船获救的最快时间为3小时.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目