Question

【题目】如图，AB是的弦，D为半径OA上的一点，过D作交弦AB于点E，交于点F，且求证：BC是的切线．

Answer 1

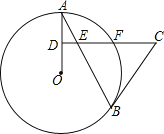
【答案】见解析

【解析】

试题连接OB，要证明BC是⊙O的切线，即要证明OB⊥BC，即要证明∠OBA+∠EBC=90°，由OA=OB，CE=CB可得：∠OBA=∠OAB，∠CBE=∠CEB，所以即要证明∠OAB+∠CEB=90°，又因为∠CEB=∠AED，所以即要证明∠OAB+∠AED=90°，由CD⊥OA不难证明.

试题解析：

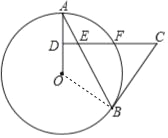
证明：连接OB，

∵OB=OA，CE=CB，

∴∠A=∠OBA，∠CEB=∠ABC，

又∵CD⊥OA，

∴∠A+∠AED=∠A+∠CEB=90°，

∴∠OBA+∠ABC=90°，

∴OB⊥BC，

∴BC是⊙O的切线.