Question

【题目】如图①是一个长为2m、宽为2n的长方形，沿图中虚线用剪刀均分成四个相同的小长方形，然后按图②的方式拼成一个正方形．

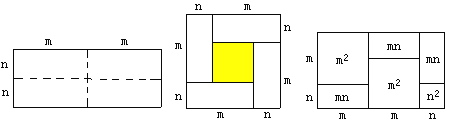
图① 图② 图③

（1）你认为图②中的阴影部分的正方形的边长等于________；

（2）请用两种不同的方法列代数式表示图②中阴影部分的面积．

方法①： ；

方法②： ；

（3）请你观察图②，利用图形的面积写出 、 ， 这三个代数式之间的等量关系： ；

（4）根据（3）中的结论，若， ，则 ；

（5）有许多代数恒等式可以用图形的面积来表示．

如图③，它表示了 ．

试画出一个几何图形，使它的面积能表示：

Answer 1

【答案】（1）；（2） ； ；（3）=；（4）

【解析】试题分析：（1）正方形的边长=小长方形的长-宽；

（2）第一种方法为：大正方形面积-4个小长方形面积，第二种表示方法为：阴影部分为小正方形的面积；

（3）利用（m+n）2-4mn=（m-n）2可求解；

（4）利用（x-y）2=（x+y）2-4xy，再求x-y，即可解答．

（5）根据多项式画出图形，即可解答．

解：（1）由图可知边长为：m-n；

（2）（m+n）2-4mn，（m-n）2；

（3）（m+n）2-4mn=（m-n）2；

（4）（x-y）2=（x+y）2-4xy，

∵x+y=-8，xy=3.75，

∴（x-y）2=64-15=49，

∴x-y=±7，

（5）如图，