题目内容
【题目】如图,已知∠AOB的大小为α,P是∠AOB内部的一个定点,且OP=2,点E、F分别是OA、OB上的动点,若△PEF周长的最小值等于2,则α=( )
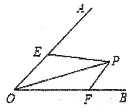
A. 30°B. 45°C. 60°D. 15°
【答案】A
【解析】
设点P关于OA的对称点为C,关于OB的对称点为D,当点E、F在CD上时,△PEF的周长为PE+EF+FP=CD,此时周长最小,根据CD=2可求出α的度数.
如图,作点P关于OA的对称点C,关于OB的对称点D,连接CD,交OA于E,OB于F.此时,△PEF的周长最小.
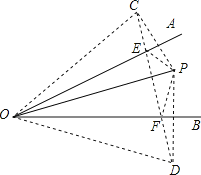
连接OC,OD,PE,PF.
∵点P与点C关于OA对称,
∴OA垂直平分PC,
∴∠COA=∠AOP,PE=CE,OC=OP,
同理,可得∠DOB=∠BOP,PF=DF,OD=OP.
∴∠COA+∠DOB=∠AOP+∠BOP=∠AOB=α,OC=OD=OP=2,
∴∠COD=2α.
又∵△PEF的周长=PE+EF+FP=CE+EF+FD=CD=2,
∴OC=OD=CD=2,
∴△COD是等边三角形,
∴2α=60°,
∴α=30°.
故选A.

【题目】某年5月,我国南方某省A、B两市遭受严重洪涝灾害,1.5万人被迫转移,邻近县市C、D获知A、B两市分别急需救灾物资200吨和300吨的消息后,决定调运物资支援灾区.已知C市有救灾物资240吨,D市有救灾物资260吨,现将这些救灾物资全部调往A、B两市.已知从C市运往A、B两市的费用分别为每吨20元和25元,从D市运往往A、B两市的费用别为每吨15元和30元,设从D市运往B市的救灾物资为x吨.
(1)请填写下表
A(吨) | B(吨) | 合计(吨) | |
C |
|
| 240 |
D |
| x | 260 |
总计(吨) | 200 | 300 | 500 |
(2)设C、D两市的总运费为w元,求w与x之间的函数关系式,并写出自变量x的取值范围;
(3)经过抢修,从D市到B市的路况得到了改善,缩短了运输时间,运费每吨减少m元(m>0),其余路线运费不变.若C、D两市的总运费的最小值不小于10320元,求m的取值范围.