题目内容
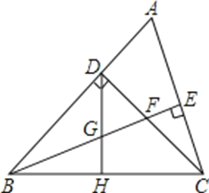
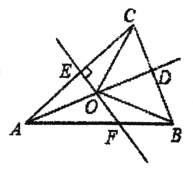
【题目】如图,在△ABC中,AB=AC,点D是C的中点,AC的垂直平分线分别交AC,AD,AB于点E,O,F.
(1)求证:点O在AB的垂直平分线上;
(2)若∠CAD=20°,求∠BOF的度数.
【答案】(1)证明见解析;(2)30°.
【解析】
(1)根据等腰三角形的性质可得AD⊥BC,根据垂直平分线的性质可得BO=AO,依此即可证明点O在AB的垂直平分线上;
(2)根据等腰三角形的性质可得∠BAD=∠CAD=20°,∠CAB=40°,再根据垂直的定义,等腰三角形的性质和角的和差故选即可得到∠BOF的度数.
(1)证明:∵AB=AC,点D是BC的中点,
∴AD⊥BC,
∵AD是BC的垂直平分线,
∴BO=CO,
∵OE是AC的垂直平分线,
∴AO=CO,
∴BO=AO,
∴点O在AB的垂直平分线上;
(2)解:∵AB=AC,点D是BC的中点,
∴AD平分∠BAC,
∵∠CAD=20°,
∴∠BAD=∠CAD=20°,∠CAB=40°,
∵OE⊥AC,
∴∠EFA=90°-40°=50°,
∵AO=CO,
∴∠OBA=∠BAD=20°,
∴∠BOF=∠EFA-∠OBA=50°-20°=30°.

练习册系列答案
相关题目