题目内容
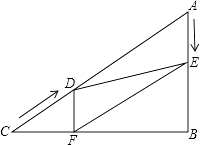
【题目】如图,△OAB是边长为2+![]() 的等边三角形,其中O是坐标原点,顶点B在y轴正方向上,将△OAB折叠,使点A落在边OB上,记为A′,折痕为EF.
的等边三角形,其中O是坐标原点,顶点B在y轴正方向上,将△OAB折叠,使点A落在边OB上,记为A′,折痕为EF.
(1)当A′E∥x轴时,求点A′和E的坐标;
(2)当A′E∥x轴,且抛物线y=﹣![]() x2+bx+c经过点A′和E时,求抛物线与x轴的交点的坐标;
x2+bx+c经过点A′和E时,求抛物线与x轴的交点的坐标;
(3)当点A′在OB上运动,但不与点O、B重合时,能否使△A′EF成为直角三角形?若能,请求出此时点A′的坐标;若不能,请你说明理由.

【答案】(1)点A′和E的坐标别是(0,1)与(![]() ,1);
,1);
(2)抛物线与x轴的交点的坐标是(![]() ,0)与(
,0)与(![]() ,0).
,0).
(3)不可能使△A′EF成为直角三角形,理由见解析.
【解析】试题分析:(1)当A′E∥x轴时,△A′EO是直角三角形,可根据∠A′OE的度数用O′A表示出OE和A′E,由于A′E=AE,且A′E+OE=OA=2+![]() ,由此可求出OA′的长,也就能求出A′E的长.据此可求出A′和E的坐标;
,由此可求出OA′的长,也就能求出A′E的长.据此可求出A′和E的坐标;
(2)将A′,E点的坐标代入抛物线中,即可求出其解析式.进而可求出抛物线与x轴的交点坐标;
(3)根据折叠的性质可知:∠FA′E=∠A,因此∠FA′E不可能为直角,因此要使△A′EF成为直角三角形只有两种可能:
①∠A′EF=90°,根据折叠的性质,∠A′EF=∠AEF=90°,此时A′与O重合,与题意不符,因此此种情况不成立.
②∠A′FE=90°,同①,可得出此种情况也不成立.
因此A′不与O、B重合的情况下,△A′EF不可能成为直角三角形.
试题解析:(1)由已知可得∠A′OE=60°,A′E=AE,
由A′E∥x轴,得△OA′E是直角三角形,
设A′的坐标为(0,b),
AE=A′E=![]() b,OE=2b,
b,OE=2b, ![]() b+2b=2+
b+2b=2+![]() ,
,
所以b=1,
所以A′、E的坐标分别是(0,1)与(![]() ,1).
,1).
(2)因为A′、E在抛物线上,
所以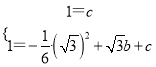 ,
,
所以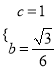 ,
,
函数关系式为y=-![]() x2+
x2+![]() x+1,
x+1,
令y=0得到:-![]() x2+
x2+![]() x+1=0,
x+1=0,
解得:x1=-![]() ,x2=2
,x2=2![]() ,
,
与x轴的两个交点坐标分别是(![]() ,0)与(2
,0)与(2![]() ,0).
,0).
(3)不可能使△A′EF成为直角三角形.
理由如下:
∵∠FA′E=∠FAE=60°,
若△A′EF成为直角三角形,只能是∠A′EF=90°或∠A′FE=90°
若∠A′EF=90°,利用对称性,则∠AEF=90°,
A、E、A三点共线,O与A重合,与已知矛盾;
同理若∠A′FE=90°也不可能,
所以不能使△A′EF成为直角三角形.