题目内容
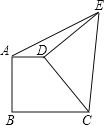
【题目】如图,在△ABC中,∠ACB=90°,D,E分别为AB,AC上一点,将△BCD,△ADE分别沿CD,DE折叠,点A、B恰好重合于点A'处.若∠A'CA=18°,则∠A=____°.

【答案】126
【解析】
由折叠的性质可得AD=A'D=BD,∠DCB=∠DCA,∠BDC=∠A'DC,∠ADE=∠EDA',由直角三角形的性质和折叠的性质可求∠DCB=54°,∠DCA=36°,即可求∠AED的度数.
解:∵将△BCD,△ADE分别沿CD,DE折叠,点A、B恰好重合于点A'处.
∴AD=A'D=BD,∠DCB=∠DCA,∠BDC=∠A'DC,∠ADE=∠EDA',
∵∠ACB=90°,AD=A'D=BD
∴AD=BD=CD,∠ACD+∠DCB=90°
∴∠A=∠DCA
∵∠ACA'=∠DCA'﹣∠DCA=18°,∠ACD+∠DCB=90°
∴∠DCB=54°,∠DCA=36°
∵∠BDC=∠A'DC,∠ADE=∠EDA',
∴∠EDC=90°
∴∠AED=∠EDC+∠DCA=126°
故答案为:126.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
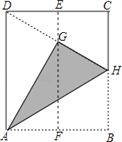
【题目】如图,在一张矩形纸片ABCD中,AD=4cm,点E,F分别是CD和AB的中点,现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH,若HG延长线恰好经过点D,则CD的长为_________.