题目内容
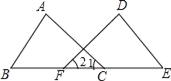
【题目】在数学实践课上,老师在黑板上画出如下的图形(其中点B、F、C、E在同一条直线上),并写出四个条件:①AB=DE,②∠1=∠2.③BF=EC,④∠B=∠E,交流中老师让同学们从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题.
(1)写出所有的真命题.(用序号表示题设、结论)
(2)请选择一个给予证明.
【答案】①答案见解析;②选择的题设:①③④;结论:②;
【解析】
①三种情况是真命题:情况一:题设①②④,结论③;由AAS证明△ABC≌△DEF,得出对应边相等BC=EF,即可得出BF=EC;情况二:题设①③④,结论②;先证BC=EF,由SAS证明△ABC≌△DEF,即可得出∠1=∠2;情况三:题设②③④,结论①;先证出BC=EF,再由ASA证明△ABC≌△DEF,即可得出AB=DE; ②选择的题设:①③④;结论:②;先证BC=EF,由SAS证明△ABC≌△DEF,即可得出∠1=∠2.
解:①情况一:题设:①②④;结论:③
情况二:题设①③④;结论:②;
情况三:题设②③④;结论:①.
②选择的题设:①③④;结论:②;
理由:∵BF=EC,
∴BF+CF=EC+CF,即BC=EF,
在△ABC和△DEF中,
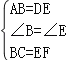 ,
,
∴△ABC≌△DEF(SAS),
∴∠1=∠2;

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
【题目】如图1是2019年11月的日历,用如图2所示的曲尺形框框(有三个方向,从左往右依次记为一、二、三个框) ,可以框住日历中的三个数,设被框住的三个数中最大的数为![]()
日 | 一 | 二 | 三 | 四 | 五 | 六 |
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

![]() 请用含
请用含![]() 的代数式填写以下三个空:第一个框框住的最小的数是_ ,第二个框框住的最小的数是__ ,第三个框框住的三个数的和是_ _.
的代数式填写以下三个空:第一个框框住的最小的数是_ ,第二个框框住的最小的数是__ ,第三个框框住的三个数的和是_ _.
![]() 这三个框分别框住的中间的数之和能恰好是
这三个框分别框住的中间的数之和能恰好是![]() 的倍数吗?如能请求出
的倍数吗?如能请求出![]() 的值,若不能请说明理由.
的值,若不能请说明理由.