题目内容
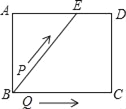
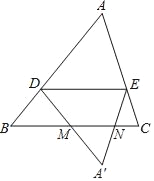
【题目】如图,在△ABC中,点D在边AB上(不与A,B重合),DE∥BC交AC于点E,将△ADE沿直线DE翻折,得到△A′DE,直线DA′,EA′分别交直线BC于点M,N.
(1)求证:DB=DM.
(2)若![]() =2,DE=6,求线段MN的长.
=2,DE=6,求线段MN的长.
(3)若![]() =n(n≠1),DE=a,则线段MN的长为 (用含n的代数式表示).
=n(n≠1),DE=a,则线段MN的长为 (用含n的代数式表示).
【答案】(1)证明见解析(2)3(3)MN=a﹣![]() (n>1)或
(n>1)或![]() ﹣a(0<n<1)
﹣a(0<n<1)
【解析】试题分析:(1)根据翻折的性质以及平行线的性质即可求证∠B=∠DMB,从而可知DB=DM;
(2)根据相似三角形的判定求证△A′MN∽△A′DE,从而![]() ,从可求出MN
,从可求出MN![]() DE=3;
DE=3;
(3)由(2)可知:△A′MN∽△A′DE,利用相似三角形的性质即可求出MN的长度,由于n没有说明情况故需要进行分类讨论.
试题解析:(1)∵DE∥BC,
∴∠ADE=∠B,∠A′DE=∠DMB,
由翻折可知:∠ADE=∠A′DE
∵∠B=∠DMB,
∴DB=DM,
(2)由翻折可知:A′D=AD
∵![]() =2,DB=DM,
=2,DB=DM,
∴![]() ,
,
∴![]() ,
,
∵DE∥BC,
∴△A′MN∽△A′DE
∴![]() ,
,
∵DE=6,
∴MN=![]() DE=3,
DE=3,
(3)由翻折可知:A′D=AD
∵![]() =n,DB=DM,
=n,DB=DM,
∴![]() =n,
=n,
当n>1时,
∴![]() ,
,
∵DE∥BC,
∴△A′MN∽△A′DE
∴![]() ,
,
∵DE=a,
∴MN=![]() DE=a﹣
DE=a﹣![]() ,
,
同理:当0<n<1时,
此时![]() ,
,
∴MN= ![]() ,
,
综上所述,MN=a﹣![]() (n>1)或
(n>1)或![]() ﹣a(0<n<1)
﹣a(0<n<1)
故答案为:(3)MN=a﹣![]() (n>1)或
(n>1)或![]() ﹣a(0<n<1)
﹣a(0<n<1)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目