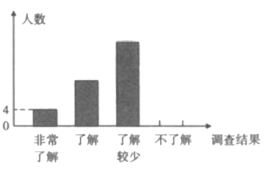
ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ‘ΡΕΝάμΫβΘ§≤ΔΜΊ¥πΈ ΧβΘΚ
»τx1Θ§x2 «ΖΫ≥Χax2+bx+cΘΫ0ΒΡΝΫΗω Β ΐΗυΘ§‘ρ”–ax2+bx+cΘΫaΘ®x©¹x1Θ©Θ®x©¹x2Θ©Θ°Φ¥ax2+bx+cΘΫax2©¹aΘ®x1+x2Θ©x+ax1x2Θ§”Ύ «bΘΫ©¹aΘ®x1+x2Θ©Θ§cΘΫax1x2Θ°”…¥ΥΩ…ΒΟ“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΒΡΗυ”κœΒ ΐΙΊœΒΘΚx1+x2ΘΫ©¹![]() Θ§x1x2ΘΫ
Θ§x1x2ΘΫ![]() Θ°’βΨΆ «Έ“Ο«÷ΎΥυ÷ή÷ΣΒΡΈΛ¥οΕ®άμΘ°
Θ°’βΨΆ «Έ“Ο«÷ΎΥυ÷ή÷ΣΒΡΈΛ¥οΕ®άμΘ°
Θ®1Θ©“―÷ΣmΘ§n «ΖΫ≥Χx2©¹x©¹100ΘΫ0ΒΡΝΫΗω Β ΐΗυΘ§≤ΜΫβΖΫ≥Χ«σm2+n2ΒΡ÷ΒΘΜ
Θ®2Θ©»τx1Θ§x2Θ§x3Θ§ «ΙΊ”ΎxΒΡΖΫ≥ΧxΘ®x©¹2Θ©2ΘΫtΒΡ»ΐΗω Β ΐΗυΘ§«“x1ΘΦx2ΘΦx3ΘΜ
ΔΌx1x2+x2x3+x3x1ΒΡ÷ΒΘΜΔΎ«σx3©¹x1ΒΡΉν¥σ÷ΒΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©201ΘΜΘ®2Θ©ΔΌ4Θ§ΔΎ![]()
ΓΨΫβΈωΓΩ
Θ®1Θ©”…Ηυ”κœΒ ΐΒΡΙΊœΒœ»ΒΟ≥ωm+nΘΫ1Θ§mnΘΫ©¹100Θ§‘Όάϊ”ΟΆξ»ΪΤΫΖΫΙΪ ΫΒΡ±δ–ΈΩ…ΒΟ¥πΑΗΘΜ
Θ®2Θ©ΔΌ”…Χβ“βΒΟΘΚxΘ®x©¹2Θ©2©¹tΘΫΘ®x©¹x1Θ©Θ®x©¹x2Θ©Θ®x©¹x3Θ©Θ§ΫΪΒ» ΫΝΫ±ΏΖ÷±π’ϊάμΘ§‘Ό±»ΫœΕ‘”ΠœνΒΡœΒ ΐΩ…ΒΟ¥πΑΗΘΜ
ΔΎœ»”…ΔΌΒΟ≥ωΒΡΫα¬έ«σΒΟx1+x3ΘΫ4©¹x2Θ§x3x1ΘΫ4©¹Θ®x1+x3Θ©x2Θ§»ΜΚσ”…![]() ΘΫ
ΘΫ![]() ©¹4x3x1ΦΑ≈δΖΫΖ®ΒΟ≥ω
©¹4x3x1ΦΑ≈δΖΫΖ®ΒΟ≥ω![]() ΒΡΉν¥σ÷ΒΘ§‘ΌΩΣΤΫΖΫΘ§«σΤδΥψ θΤΫΖΫΗυΦ¥Ω…Θ°
ΒΡΉν¥σ÷ΒΘ§‘ΌΩΣΤΫΖΫΘ§«σΤδΥψ θΤΫΖΫΗυΦ¥Ω…Θ°
ΫβΘΚΘ®1Θ©ΓΏmΘ§n «ΖΫ≥Χx2©¹x©¹100ΘΫ0ΒΡΝΫΗω Β ΐΗυ
Γύm+nΘΫ1Θ§mnΘΫ©¹100
Γύm2+n2ΘΫΘ®m+nΘ©2©¹2mn
ΘΫ12©¹2ΓΝΘ®©¹100Θ©
ΘΫ201ΘΜ
Θ®2Θ©ΔΌ”…Χβ“βΒΟΘΚxΘ®x©¹2Θ©2©¹tΘΫΘ®x©¹x1Θ©Θ®x©¹x2Θ©Θ®x©¹x3Θ©
Γύx3©¹4x2+4x©¹tΘΫx3©¹Θ®x1+x2+x3Θ©x2+Θ®x1x2+x2x3+x3x1Θ©x©¹x1x2x3
Γύx1+x2+x3ΘΫ4Θ§x1x2+x2x3+x3x1ΘΫ4Θ§x1x2x3ΘΫt
Γύx1x2+x2x3+x3x1ΒΡ÷ΒΈΣ4ΘΜ
ΔΎΓΏx1+x2+x3ΘΫ4
Γύx1+x3ΘΫ4©¹x2
ΓΏx1x2+x2x3+x3x1ΘΫ4
Γύx3x1ΘΫ4©¹Θ®x1+x3Θ©x2
ΓΏ![]() ΘΫ
ΘΫ![]() ©¹4x3x1
©¹4x3x1
Γύ![]() ΘΫ
ΘΫ![]() ©¹4[4©¹Θ®x1+x3Θ©x2]
©¹4[4©¹Θ®x1+x3Θ©x2]
ΘΫ©¹3![]() +8x2
+8x2
ΘΫ©¹3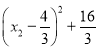 Γή
Γή![]()
ΓύΒ±x2ΘΫ![]() ±Θ§x3©¹x1ΒΡΉν¥σ÷ΒΈΣΘΚ
±Θ§x3©¹x1ΒΡΉν¥σ÷ΒΈΣΘΚ![]() ΘΫ
ΘΫ![]() Θ°
Θ°
Γύx3©¹x1ΒΡΉν¥σ÷ΒΈΣ![]() Θ°
Θ°

 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗΓΨΧβΡΩΓΩΡ≥–ΘΈΣΝΥΫβΑΥΡξΦΕ―ß…ζΥ·ΟΏ ±ΦδΒΡ«ιΩωΘ§ΥφΜζΒς≤ιΝΥΗΟ–ΘΑΥΡξΦΕ 50 Οϊ―ß…ζΘ§ΒΟΒΫΝΥ“ΜΧλΥ·ΟΏ ±ΦδΒΡ“ΜΉι―υ±Ψ ΐΨίΘ§»γœ¬ΘΚ
Υ·ΟΏ ±Φδ | Ήι÷–÷Β | ΤΒ ΐ |
|
| 3 |
| 6 | 3 |
| 7 |
|
| 8 | 25 |
| 9 | 10 |
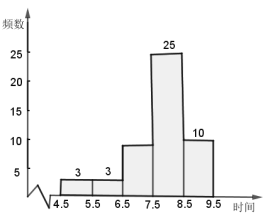
ΗυΨί“‘…œΆ≥ΦΤΆΦ±μΆξ≥…œ¬Ν–Έ ΧβΘΚ
Θ®1Θ©Ά≥ΦΤ±μ÷–![]() ΘΜ
ΘΜ![]() ΘΜ
ΘΜ
Θ®2Θ©ΗυΨί ΐΨίΘ§ΙάΥψΗΟ–ΘΑΥΡξΦΕ―ß…ζΤΫΨυΟΩΧλΥ·ΟΏ ±ΦδΘΜ
Θ®3Θ©Υ·ΟΏ ±ΦδΈΣ 4.5~5.5h ΒΡ 3 ΟϊΆ§―ß÷–”– 1 ΟϊΡ–…ζΚΆ 2 Οϊ≈°…ζΘ§œ÷¥”÷–ΥφΜζΧτ―Γ 2 ΟϊΆ§―ß»Ξ“Ϋ‘ΚΫχ––ΫΓΩΒΧεΦλΘ§«κ”Ο ςΉ¥ΆΦΖ®ΜρΝ–±μΖ®«σ≥ω«ΓΚΟ―Γ÷–ΓΑ1 Ρ– 1 ≈°Γ±ΒΡΗ≈¬ Θ°