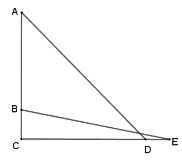
题目内容
【题目】如图，在
中，
，
是
边上的动点(不与点
重合)，将
沿
所在的直线翻折，得到
，连接
，则下列判断：
①当
时，
②当时，
③当
时，
；
④长度的最小值是1．
其中正确的判断是______(填入正确结论的序号)
【答案】①②④
【解析】
①由直角三角形斜边上的中线等于斜边的一半以及折叠的性质，易得
，即可得
;
②由
，可得点
在以
为圆心，
长为半径的圆上，然后在由圆周角定理，求得答案;
③当
时，易得
，再根据相似三角形对应边成比例，求得AP的长;
④易得
，
长度的最小值是1．
解：①∵在
中，
，
∴
，
，
由折叠的性质可得：
∴
，
∴
∴；故①正确；
②∵
，
∴，
∴点在以为圆心，长为半径的圆上，
∵由折叠的性质可得：
，
∴
，
∴
故②正确
③当时，
，
∵
，
∴，
∴
∵在
中，由勾股定理可知
∴
故③错误；
④由轴对称的性质可知：
，
∵
长度固定不变，
∵
∴
的长度有最小值．
有最小值
．故④正确．
故答案为：①②④
练习册系列答案
教材全解字词句篇系列答案
相关题目
【题目】二次函数
上部分点的横坐标x与纵坐标y的对应值如下表：
x | … |
|
| 0 | 1 | 2 | 3 | … |
y | … | 3 |
| 0 |
| 0 | m | … |
（1）直接写出此二次函数的对称轴 ；
（2）求b的值；
（3）直接写出表中的m值，m= ；
（4）在平面直角坐标系xOy中，画出此二次函数的图象．
