题目内容
已知：如图，P是矩形ABCD的CD边上一点，PE⊥AC于E，PF⊥BD于F，AC=15，BC=8，求PE+PF．
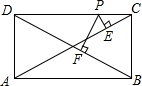
∵四边形ABCD是矩形，
∴BD=AC=15，OD=OC，
∴设∠BDC=∠DCA=α，
在Rt△PCE中，sin∠DCA=sinα=
，
∴PE=PCsinα，
在Rt△PDF中，sin∠BDC=sinα=
，
∴PF=PDsinα，
∴PE+PF=PCsinα+PDsinα=CDsinα，
∵在Rt△BCD中，BD=15，BC=8，
∴sinα=
，CD=
=
，
∴PE+PF=
×
=
．
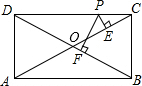
∴BD=AC=15，OD=OC，
∴设∠BDC=∠DCA=α，
在Rt△PCE中，sin∠DCA=sinα=
| PE |
| PC |
∴PE=PCsinα，
在Rt△PDF中，sin∠BDC=sinα=
| PF |
| DP |
∴PF=PDsinα，
∴PE+PF=PCsinα+PDsinα=CDsinα，
∵在Rt△BCD中，BD=15，BC=8，
∴sinα=
| 8 |
| 15 |
| BD2-BC2 |
| 161 |
∴PE+PF=
| 161 |
| 8 |
| 15 |
8
| ||
| 15 |
练习册系列答案
相关题目
速度不变，它再航行多长时间可以到达小岛M？（
要使教学楼不受货车的噪声影响，在此路段应该限速多少？（精确到10km/h）