题目内容
光明路新华书店为了提倡人们“多读书,读好书”,每年都要开展分年级免费赠书活动,今年获得免费赠书的前提是:顺利通过书店前的A,B,C三个房间(在每个房间内都有一道题,若能在规定的时间内顺利答对这三道题,就可免费得到赠书),同学们你们想参加吗?快快行动吧!
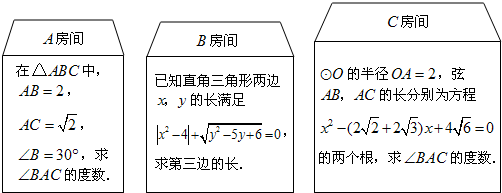
题目并不难哟,把答案写在下面吧!A房间答题卡:______;B房间答题卡:______;C房间答题卡:______.

题目并不难哟,把答案写在下面吧!A房间答题卡:______;B房间答题卡:______;C房间答题卡:______.
A:如图1,过点A作AD⊥BC,交于点D,
∵在△ABC中,AB=2,AC=
,∠B=30°,
∴AD=
AB=1,
∠BAD=90°-30°=60°,
∴cos∠CAD=
=
=
,
∴∠CAD=45°,
∴∠BAC=60°+45°=105°,
如图2,
同理得出:∠BAD=60°,∠CAD=45°,
∴∠BAC=60°-45°=15°,
故答案为:105°或15°;
B.∵直角三角形两边满足|x2-4|+
=0,
∴x2-4=0,y2-5y+6=0,
∴解得:x=2或-2(不合题意舍去),
y=2或3,
∴当两直角边为:2,2,则斜边为:2
,
当两直角边为:2,3,则斜边为:
=
,
当斜边为3,一直角边为2,则另一直角边为:
=
,
故答案为:2
或
或
;
C.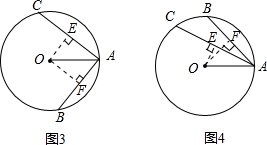 ∵⊙O的半径为2,弦AC,AB的长是方程x2-(2
∵⊙O的半径为2,弦AC,AB的长是方程x2-(2
+2
)x+4
=0的两根,
∴x2-(2
+2
)x+4
=0,
(x-2
)(x-2
)=0,
∴解得:x1=2
,x2=2
,
∴设AC=2
,AB=2
,
过点作OE⊥AC,OF⊥AB,
∴AE=EC=
,AF=FB=
,
∴cos∠FAO=
=
,
∴∠FAO=45°,
cos∠EAO=
=
,
∴∠EAO=30°,
∴∠BAC=∠FAO+∠EAO=30°+45°=75°,
结合图4,同理可得出:
过点作OE⊥AC,OF⊥AB,
∴AE=EC=
,AF=FB=
,
∴cos∠FAO=
=
,
∴∠FAO=45°,
cos∠EAO=
=
,
∴∠EAO=30°,
∴∠BAC=∠FAO-∠EAO=45°-30°=15°,
故答案为:15°或75°.

∵在△ABC中,AB=2,AC=
| 2 |
∴AD=
| 1 |
| 2 |
∠BAD=90°-30°=60°,
∴cos∠CAD=
| AD |
| AC |
| 1 | ||
|
| ||
| 2 |
∴∠CAD=45°,
∴∠BAC=60°+45°=105°,
如图2,
同理得出:∠BAD=60°,∠CAD=45°,
∴∠BAC=60°-45°=15°,
故答案为:105°或15°;
B.∵直角三角形两边满足|x2-4|+
| y2-5y+6 |
∴x2-4=0,y2-5y+6=0,
∴解得:x=2或-2(不合题意舍去),
y=2或3,
∴当两直角边为:2,2,则斜边为:2
| 2 |
当两直角边为:2,3,则斜边为:
| 22+32 |
| 13 |
当斜边为3,一直角边为2,则另一直角边为:
| 32-22 |
| 5 |
故答案为:2
| 2 |
| 13 |
| 5 |
C.
 ∵⊙O的半径为2,弦AC,AB的长是方程x2-(2
∵⊙O的半径为2,弦AC,AB的长是方程x2-(2| 2 |
| 3 |
| 6 |
∴x2-(2
| 2 |
| 3 |
| 6 |
(x-2
| 2 |
| 3 |
∴解得:x1=2
| 2 |
| 3 |
∴设AC=2
| 3 |
| 2 |
过点作OE⊥AC,OF⊥AB,
∴AE=EC=
| 3 |
| 2 |
∴cos∠FAO=
| AF |
| AO |
| ||
| 2 |
∴∠FAO=45°,
cos∠EAO=
| EA |
| AO |
| ||
| 2 |
∴∠EAO=30°,
∴∠BAC=∠FAO+∠EAO=30°+45°=75°,
结合图4,同理可得出:
过点作OE⊥AC,OF⊥AB,
∴AE=EC=
| 3 |
| 2 |
∴cos∠FAO=
| AF |
| AO |
| ||
| 2 |
∴∠FAO=45°,
cos∠EAO=
| EA |
| AO |
| ||
| 2 |
∴∠EAO=30°,
∴∠BAC=∠FAO-∠EAO=45°-30°=15°,
故答案为:15°或75°.


练习册系列答案
相关题目


 速度不变,它再航行多长时间可以到达小岛M?(
速度不变,它再航行多长时间可以到达小岛M?(

 方程x2-7x+12=0的两个根,且OA>OB;
方程x2-7x+12=0的两个根,且OA>OB;