题目内容
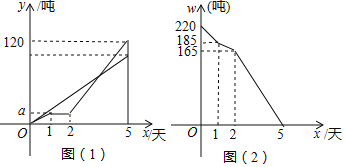
【题目】某市制米厂接到加工大米任务,要求5天内加工完220吨大米,制米厂安排甲、乙两车间共同完成加工任务,乙车间加工中途停工一段时间维修设备,然后改变加工效率继续加工,直到与甲车间同时完成加工任务为止.设甲、乙两车间各自加工大米数量y(吨)与甲车间加工时间s(天)之间的关系如图(1)所示;未加工大米w(吨)与甲加工时间x(天)之间的关系如图(2)所示,请结合图象回答下列问题:
(1)甲车间每天加工大米 吨,a= .
(2)求乙车间维修设备后,乙车间加工大米数量y(吨)与x(天)之间函数关系式.
(3)若55吨大米恰好装满一节车厢,那么加工多长时间装满第一节车厢?再加工多长时间恰好装满第二节车厢?
【答案】(1)20,15;(2)y=35x﹣55;(3)再过1天装满第二节车厢.
【解析】(1)根据题意,由图2得出两个车间同时加工和甲单独加工的速度;
(2)用待定系数法解决问题;
(3)求出两个车间每天加工速度分别计算两个55吨完成的时间.
(1)由图象可知,第一天甲乙共加工220﹣185=35吨,
第二天,乙停止工作,甲单独加工185﹣165=20吨,
则乙一天加工35﹣20=15吨,a=15,
故答案为:20,15;
(2)设y=kx+b,
把(2,15),(5,120)代入得![]() ,
,
解得:![]() ,
,
∴y=35x﹣55(2≤x≤5);
(3)①当0<x≤1时,20+15=35<55,不合理,
②当1<x≤2是地,20x+15=55,x=2,
③当2<x≤5时,20x+35x-55=110,x=3,
3-2=1(天),
所以生产2天可装满第一节车厢,再经过1天可装满第二节车厢.

【题目】在一个不透明的口袋里装着只有颜色不同的黑、白两种颜色的球共50只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复以上步骤,下表为实验的一组统计数据:
摸球的次数n | 1000 | 1500 | 2000 | 5000 | 8000 | 10000 |
摸到白球的次数m | 582 | 960 | 1161 | 2954 | 4842 | 6010 |
摸到白球的频率 | 0.582 | 0.64 | 0.5805 | 0.5908 | 0.6053 | 0.601 |
请估算口袋中白球的个数约为( )
A. 20 B. 25 C. 30 D. 35
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第![]() (1≤
(1≤![]() ≤90)天的售价与销量的相关信息如下表:
≤90)天的售价与销量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200﹣2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为![]() 元.
元.
(1)求出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.