Question

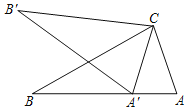
【题目】如图，等腰△ABC中AB＝BC，将△ABC绕点C顺时针旋转α角时，点A的对应点A′恰好落在AB边上，则∠A′CB＝_____（用含α的式子来表示）．

Answer 1

【答案】90°﹣α

【解析】

由旋转确定∠ACA′＝α，CA＝CA′，再利用等腰三角形的性质得到∠ACB＝∠A＝（180°﹣α），再用角度差得到∠A′CB＝∠ACB﹣∠A′CA=90°﹣α.

∵将△ABC绕点C顺时针旋转α角时，点A的对应点A′恰好落在AB边上，

∴∠ACA′＝α，CA＝CA′，

∴∠A＝（180°﹣∠A′CA）＝（180°﹣α），

∵AB＝BC，

∴∠ACB＝∠A＝（180°﹣α），

∴∠A′CB＝∠ACB﹣∠A′CA＝（180°﹣α）﹣α＝90°﹣α，

故答案为：90°﹣α．