��Ŀ����
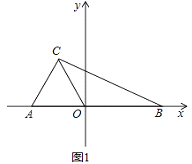
����Ŀ����ƽ��ֱ������ϵ�У�A��a��0����B��b��0����C����1��2������ͼ1������ ![]()
��1����a��b��ֵ��
��2������x����������ϴ���һ��M��ʹ������COM�������������ABC�������һ�룬�����M�����ꣻ
���������������λ���Ƿ���ڵ�M��ʹ������COM�����������ABC�������һ����Ȼ����? �����ڣ���ֱ��д�����������ĵ�M�����ꣻ
��3����ͼ2������C��CD��y�ύy���ڵ�D����PΪ�߶�CD�ӳ����ϵ�һ���㣬����OP��OEƽ�֡�AOP��OF��OE������P�˶�ʱ�� ![]() ��ֵ�Ƿ��ı䣿�����䣬����ֵ�����ı䣬˵�����ɣ�
��ֵ�Ƿ��ı䣿�����䣬����ֵ�����ı䣬˵�����ɣ�

���𰸡���1��a=-2��b=3����2�����������ĵ�M����Ϊ��2.5��0����-2.5��0����0��5����0��-5������3��![]() =2�����ɼ�������
=2�����ɼ�������
�����������������
��1����![]() �г�����a��b�ķ����飬���ɽ��a��b��ֵ��
�г�����a��b�ķ����飬���ɽ��a��b��ֵ��
��2�������������M������Ϊ��x��0������OM=![]() �������COM������ǡ�ABC�����һ�룬�г����̣��ⷽ�̽�ϵ�M��x��������ἴ����ô�ʱ��M�����ꣻ
�������COM������ǡ�ABC�����һ�룬�г����̣��ⷽ�̽�ϵ�M��x��������ἴ����ô�ʱ��M�����ꣻ
�������еĽ���ɵõ�M��x�Ḻ����ʱ�����ꣻ��M��y����ʱ�������M������Ϊ��0��y������ϡ�COM������ǡ�ABC�����һ�룬�г����̣��ⷽ�̼�����õ�M��y���ϵķ������������ꣻ
��3����������֤��OPD=��POB=2��BOF����DOE+��DOF=90������BOF+��DOF=90�����ɴ˿ɵõ���OPD=2��BOF=2��DOE���Ӷ��ɵ�![]() =2.
=2.
���������
��1����![]() ��
��
��![]() �����
�����![]() ��
��
��2��������1���н��ۿ�֪��A��B������ֱ�Ϊ��-2��0���ͣ�3��0����
��AB=5��
�֡ߵ�C������Ϊ��-1��2����
��S��ABC=![]() ��
��
����M��x����ʱ�����M������Ϊ��x��0������OM=![]() ��������ɵã�
��������ɵã�
![]() �����
�����![]() ��
��
����M��x��������ᣬ
����M��������2.5��0����
�������н��ۿ�֪����M��x��ĸ�����ʱ����M������Ϊ��-2.5��0����
����M��y����ʱ������ͼ�������M������Ϊ��0��y������OM=![]() ��������ɵã�
��������ɵã�
![]() ����ã�
����ã� ![]() ��
��
����ʱ��M������Ϊ��0��5����0��-5����
��������������M����������ʱ��������ֱ�Ϊ��2.5��0������-2.5��0������0��5���ͣ�0��-5����
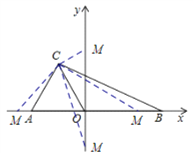
��3����ͼ2����CD��y�ᣬ
��CD��OB��
���OPD=��POB��
��OFƽ����POB��
���OPD=��POB=2��BOF��
��OE��OF��
���EOF=��DOB=90����
���DOE+��DOF=��DOF+��BOF=90����
���DOE=��BOF��
���POD=2��DOE��
��![]() =2.
=2.

 Сѧ���AB��ϵ�д�
Сѧ���AB��ϵ�д�