Question

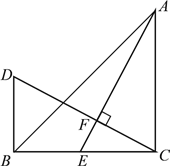
【题目】如图，Rt△ABC中，∠C=90°，AD平分∠CAB，DE⊥AB于E，若AC=6，BC=8，CD=3．

（1）求DE的长；

（2）求△ADB的面积．

Answer 1

【答案】解：（1）∵AD平分∠CAB，DE⊥AB，∠C=90°，

∴CD=DE，

∵CD="3" ，

∴DE=3；

（2）在Rt△ABC中，由勾股定理得：AB=AC+BC=6+8=10，∴AB=10，

∴△ADB的面积为S△ADB=ABDE=×10×3=15．

【解析】试题分析：（1）根据角平分线性质得出CD=DE，代入求出即可；

（2）利用勾股定理求出AB的长，然后计算△ADB的面积．

解：（1）∵AD平分∠CAB，DE⊥AB，∠C=90°，

∴CD=DE，

∵CD=3，

∴DE=3；

（2）在Rt△ABC中，由勾股定理得：AB===10，

∴△ADB的面积为S△ADB=ABDE=×10×3=15．