��Ŀ����
����Ŀ��̽�������⣺
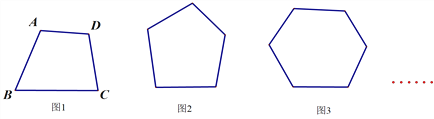
(1)���������
��ͼ1������A�������__________���Խ��ߣ�ͬ��������B�������__________��������C�������__________��������D�������__________���Խ���.
ͨ�����Ϸ������ܽᣬͼ1����___________���Խ���.
��2����չ���죺
���ã�1���ķ����������ɵã�
ͼ2����_____________���Խ��ߣ�
ͼ3����_____________���Խ��ߣ�
(3)̽�����ɣ�
����n����(n>3)������_____________���Խ��ߣ�(�ú�n��ʽ�ӱ�ʾ)
(4)������֤��
ʮ������__________________�Խ���.
���𰸡� 1 1 1 1 2 5 9 ![]() 35
35
���������������:(1)���ݶԽ��ߵĶ���,�ı��ξ�������һ�������1���Խ���,���л�����ظ�,����ı��ι���2���Խ���,(2)����ξ�������һ�������2���Խ���,���л�����ظ�,����ı��ι���5���Խ���, �����ξ�������һ�������3���Խ���,���л�����ظ�,����ı��ι���9���Խ���,(3) n���ξ�������һ�������(n��3)���Խ���,���л�����ظ�,����ı��ι���![]() ���Խ���,(4) ʮ���ξ�������һ�������7���Խ���,���л�����ظ�,����ı��ι���35���Խ���.
���Խ���,(4) ʮ���ξ�������һ�������7���Խ���,���л�����ظ�,����ı��ι���35���Խ���.
�������:(1) �ı��ξ�������һ�������1���Խ���,���л�����ظ�,����ı��ι���2���Խ���,
(2)����ξ�������һ�������2���Խ���,���л�����ظ�,����ı��ι���5���Խ���, �����ξ�������һ�������3���Խ���,���л�����ظ�,����ı��ι���9���Խ���,
(3) n���ξ�������һ�������(n��3)���Խ���,���л�����ظ�,����ı��ι���![]() ���Խ���,
���Խ���,
(4) ʮ���ξ�������һ�������7���Խ���,���л�����ظ�,����ı��ι���35���Խ���.

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�