��Ŀ����
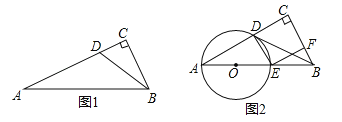
����Ŀ����ͼ1��Rt��ACB �У���C=90������D��AC�ϣ���CBD=��A����A��D�����Բ��Բ��O��AB�ϣ�
��1������ֱ�ߺ�Բ����ͼ1�л�����O����д������������ͼ�ۼ������ú�ɫˮ�ʰ��������������
��2���ж�BD����ֱ���루1������������O��λ�ù�ϵ����֤����Ľ��ۣ�
��3������O��AB�ڵ�E������DE������E��EF��BC��FΪ���㣬����D���߶�AC�Ļƽ�ָ�㣨��![]() ������ͼ2����˵���ı���DEFC�������Σ�
������ͼ2����˵���ı���DEFC�������Σ�
���𰸡���1����ͼ����������2��BD���O���У���3��֤����������
�������������������1����ͼ1�����߶�AD�Ĵ�ֱƽ���߽�AB��O��Ȼ���Ե�OΪԲ�ģ�OAΪ�뾶��Բ��
��2������OD����ͼ1��������A=��ODA����CBD=��A�õ���CBD=��ODA�����֤����ODB=90����Ȼ��������ߵ��ж��������ж�BDΪ��O�����ߣ�
��3����֤����CDB�ס�CBA�õ�CB2=CDCA���ٸ��ݻƽ�ָ�Ķ���õ�AD2=CDAC����AD=CB������֤����ADE�ա�BCD�õ�DE=DC�����ı���CDEFΪ���Σ�Ȼ����������ε��ж��������ж��ı���DEFC�������Σ�
����������⣺��1����ͼ1����OΪ������

��2��BD����O���У��������£�
����OD����ͼ1����OA=OD�����A=��ODA���ߡ�CBD=��A�����CBD=��ODA���ߡ�C=90�������CBD+��CDB=90�������ODA+��CDB=90�������ODB=90������OD��BD����BDΪ��O�����ߣ�
��3���ߡ�CBD=��A����DCB=��BCA�����CDB�ס�CBA����CD��CB=CB��CA����CB2=CDCA������D���߶�AC�Ļƽ�ָ�㣬��AD2=CDAC����AD=CB����AEΪֱ�������ADE=90��������ADE����BCD�����ߡ�A=��CBD��AD=BC����ADE=��C�����ADE�ա�BCD����DE=DC����EF��BC�����EFC=90�������ı���CDEFΪ���Σ����ı���DEFC�������Σ�