题目内容
如图，小明在坡度为1：2.4的山坡AB上的A处测得大树CD顶端D的仰角为45°，CD垂直于水平面，测得坡面AB长为13米，BC长为9米，A、B、C、D在一个平面内，求树高CD．
作AD⊥BC延长线于点D，AE垂直大树与点E，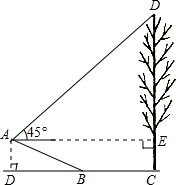
∵山坡AB的坡比为1：2.4，
∴
=1：2.4，
设AD=x，则BD=2.4x，
在Rt△ADB中，AD2+BD2=AB2=132，即x2+（2.4x）2=132，
解得x=5，
则BD=2.4x=12米，
∵BC=9米，
∴DC=12+9=21米，
∵四边形ADCE为矩形，
∴AE=DC=21米，
∵山坡AB上的A处测得大树CD顶端D的仰角为45°，
∴
=tan45°，
∴DE=AE•tan45°=21米，
则DC=ED+EC=21+5=26米．
答：树高为26米．
∵山坡AB的坡比为1：2.4，
∴
| AD |
| BD |
设AD=x，则BD=2.4x，
在Rt△ADB中，AD2+BD2=AB2=132，即x2+（2.4x）2=132，
解得x=5，
则BD=2.4x=12米，
∵BC=9米，
∴DC=12+9=21米，
∵四边形ADCE为矩形，
∴AE=DC=21米，
∵山坡AB上的A处测得大树CD顶端D的仰角为45°，
∴
| ED |
| AE |
∴DE=AE•tan45°=21米，
则DC=ED+EC=21+5=26米．
答：树高为26米．
练习册系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
