题目内容
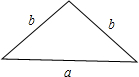
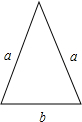
一个三角形的边长分别为a，a，b，另一个三角形的边长分别为b，b，a，其中a＞b，若两个三角形的最小内角相等，
的值等于（ ）
| a |
| b |
A．
| B．
| C．
| D．
|
余弦定理：a，a，b中最小内角为边b所对，cosx=
b，b，a中最小内角为边b所对，cosy=
∵x=y，
∴
=
解方程得：
=
．
故选B．
| a2+a2-b2 |
| 2a2 |
b，b，a中最小内角为边b所对，cosy=
| b2+a2-b2 |
| 2ab |
∵x=y，
∴
| a2+a2-b2 |
| 2a2 |
| b2+a2-b2 |
| 2ab |
解方程得：
| a |
| b |
| ||
| 2 |
故选B．
练习册系列答案
文敬图书课时先锋系列答案
相关题目
