Question

【题目】已知四边形ABCD是菱形，AB=4，∠ABC=60°，∠EAF的两边分别与射线CB，DC相交于点E，F，且∠EAF=60°．

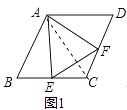
（1）如图1，当点E是线段CB的中点时，直接写出线段AE，EF，AF之间的数量关系；
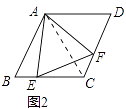
（2）如图2，当点E是线段CB上任意一点时（点E不与B、C重合），求证：BE=CF；
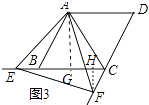
（3）如图3，当点E在线段CB的延长线上，且∠EAB=15°时，求点F到BC的距离．

Answer 1

【答案】
（1）

解：结论AE=EF=AF．

理由：如图1中，连接AC，

∵四边形ABCD是菱形，∠B=60°，

∴AB=BC=CD=AD，∠B=∠D=60°，

∴△ABC，△ADC是等边三角形，

∴∠BAC=∠DAC=60°

∵BE=EC，

∴∠BAE=∠CAE=30°，AE⊥BC，

∵∠EAF=60°，

∴∠CAF=∠DAF=30°，

∴AF⊥CD，

∴AE=AF（菱形的高相等），

∴△AEF是等边三角形，

∴AE=EF=AF

（2）

证明：连接AC，如图2中，∵∠BAC=∠EAF=60°，

∴∠BAE=∠CAE，

在△BAE和△CAF中，

，

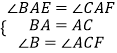∴△BAE≌△CAF，

∴BE=CF

（3）

解：过点A作AG⊥BC于点G，过点F作FH⊥EC于点H，

∵∠EAB=15°，∠ABC=60°，

∴∠AEB=45°，

在RT△AGB中，∵∠ABC=60°，AB=4，

∴BG= AB=2，AG= BG=2 ，

在RT△AEG中，∵∠AEG=∠EAG=45°，

∴AG=GE=2 ，

∴EB=EG﹣BG=2 ﹣2，

∵△AEB≌△AFC，

∴AE=AF，EB=CF=2 ﹣2，

在RT△CHF中，∵∠HCF=180°﹣∠BCD=60°，CF=2 ﹣2，

∴FH=CFsin60°=（2 ﹣2） =3﹣ ．

∴点F到BC的距离为3﹣ ．

【解析】（1）结论AE=EF=AF．只要证明AE=AF即可证明△AEF是等边三角形．（2）欲证明BE=CF，只要证明△BAE≌△CAF即可．（3）过点A作AG⊥BC于点G，过点F作FH⊥EC于点H，根据FH=CFcos30°，因为CF=BE，只要求出BE即可解决问题．