Question

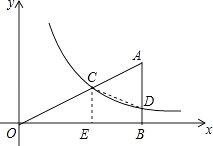
【题目】如图，Rt△ABO的顶点O在坐标原点，点B在x轴上，∠ABO=90°，∠AOB=30°，OB=2 ，反比例函数y= （x＞0）的图象经过OA的中点C，交AB于点D．
（1）求反比例函数的关系式；
（2）连接CD，求四边形CDBO的面积．

Answer 1

【答案】
（1）解：∵∠ABO=90°，∠AOB=30°，OB=2 ，

∴AB= OB=2，

作CE⊥OB于E，

∵∠ABO=90°，

∴CE∥AB，

∴OC=AC，

∴OE=BE= OB= ，CE= AB=1，

∴C（ ，1），

∵反比例函数y= （x＞0）的图象经过OA的中点C，

∴1= ，

∴k= ，

∴反比例函数的关系式为y=

（2）解：∵OB=2 ，

∴D的横坐标为2 ，

代入y= 得，y= ，

∴D（2 ， ），

∴BD= ，

∵AB=2，

∴AD= ，

∴S△ACD= ADBE= × × = ，

∴S四边形CDBO=S△AOB﹣S△ACD= OBAB﹣ = ×2 ×2﹣ = ．

【解析】（1）解直角三角形求得AB，作CE⊥OB于E，根据平行线分线段成比例定理和三角形中位线的性质求得C的坐标，然后根据待定系数法即可求得反比例函数的解析式；（2）求得D的坐标，进而求得AD的长，得出△ACD的面积，然后根据S四边形CDBO=S△AOB﹣S△ACD即可求得．