题目内容
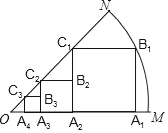
【题目】如图,已知△ABC内接于⊙O,BC交直径AD于点E,过点C作AD的垂线交AB的延长线于点G,垂足为F.连接OC.
(1)若∠G=48°,求∠ACB的度数;
(2)若AB=AE,求证:∠BAD=∠COF;
(3)在(2)的条件下,连接OB,设△AOB的面积为S1,△ACF的面积为S2.若tan∠CAF=![]() ,求
,求![]() 的值.
的值.

【答案】(1)48°(2)证明见解析(3)![]()
【解析】
(1)连接CD,根据圆周角定理和垂直的定义可得结论;
(2)先根据等腰三角形的性质得:∠ABE=∠AEB,再证明∠BCG=∠DAC,可得 ![]() ,则所对的圆周角相等,根据同弧所对的圆周角和圆心角的关系可得结论;
,则所对的圆周角相等,根据同弧所对的圆周角和圆心角的关系可得结论;
(3)过O作OG⊥AB于G,证明△COF≌△OAG,则OG=CF=x,AG=OF,设OF=a,则OA=OC=2x-a,根据勾股定理列方程得:(2x-a)2=x2+a2,则a=![]() x,代入面积公式可得结论.
x,代入面积公式可得结论.
(1)连接CD,
∵AD是⊙O的直径,
∴∠ACD=90°,
∴∠ACB+∠BCD=90°,
∵AD⊥CG,
∴∠AFG=∠G+∠BAD=90°,
∵∠BAD=∠BCD,
∴∠ACB=∠G=48°;
(2)∵AB=AE,
∴∠ABE=∠AEB,
∵∠ABC=∠G+∠BCG,∠AEB=∠ACB+∠DAC,
由(1)得:∠G=∠ACB,
∴∠BCG=∠DAC,
∴![]() ,
,
∵AD是⊙O的直径,AD⊥PC,
∴![]() ,
,
∴![]() ,
,
∴∠BAD=2∠DAC,
∵∠COF=2∠DAC,
∴∠BAD=∠COF;
(3)过O作OG⊥AB于G,设CF=x,
∵tan∠CAF=![]() =
=![]() ,
,
∴AF=2x,
∵OC=OA,由(2)得:∠COF=∠OAG,
∵∠OFC=∠AGO=90°,
∴△COF≌△OAG,
∴OG=CF=x,AG=OF,
设OF=a,则OA=OC=2x﹣a,
Rt△COF中,CO2=CF2+OF2,
∴(2x﹣a)2=x2+a2,
a=![]() x,
x,
∴OF=AG=![]() x,
x,
∵OA=OB,OG⊥AB,
∴AB=2AG=![]() x,
x,
∴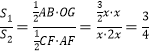 .
.

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案