题目内容
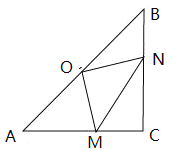
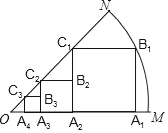
【题目】如图所示，扇形OMN的圆心角为45°，正方形A1B1C1A2的边长为2，顶点A1，A2在线段OM上，顶点B1在弧MN上，顶点C1在线段ON上，在边A2C1上取点B2，以A2B2为边长继续作正方形A2B2C2A3，使得点C2在线段ON上，点A3在线段OM上，……，依次规律，继续作正方形，则A2018M=__________．
【答案】
．
【解析】
探究规律，利用规律即可解决问题.
∵∠MON=45°，
∴△C1B2C2为等腰直角三角形，
∴C1B2=B2C2=A2B2．
∵正方形A1B1C1A2的边长为2，
∴OA3=AA3=A2B2=
A2C1=1．OA1=4，OM=OB1=
，
同理，可得出：OAn=An-1An=An-2An-1=
，
∴OA2018=A2018A2017=
，
∴A2018M=2
-．
故答案为2-．
练习册系列答案
相关题目
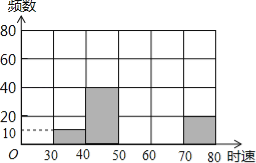
【题目】将某雷达测速区监测到的一组汽车的时速数据整理，得到其频数分布表（未完成）：
数据段 | 30～40 | 40～50 | 50～60 | 60～70 | 70～80 | 总计 |
频 数 | 10 | 40 | | | 20 | |
百分比 | 5% | | 40% | | 10% | |
注：30～40为时速大于等于30千米而小于40千米，其他类同．
（1）请你把表中的数据填写完整；
（2）补全频数分布直方图；
（3）如果此路段汽车时速超过60千米即为违章，则违章车辆共有多少辆？
