Question

【题目】如图，抛物线与轴的正半轴交于点．

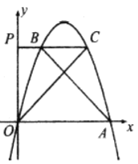
（1）求点的坐标和该抛物线的对称轴．

（2）点在轴的正半轴上，轴交抛物线于点、（点在点的左侧），设，

①当是的中点时，求的值；

②连结，设与的周长之差为，求关于的函数表达式．

Answer 1

【答案】（1）；对称轴为直线；（2）①；②

【解析】

（1）令，解方程即可求出点的坐标，根据二元一次方程的对称轴即可求出抛物线的对称轴；

（2）①把的坐标用的代数式表示并代入抛物线即可求出的值；

②根据抛物线的对称性，可知AB=OC，与的周长之差可转化为OA和BC的差．

解：（1）令，，解得，（不符合题意），

∴；

由抛物线可知，，，

∴对称轴为直线．

（2）①∵是的中点，∴，

把代入抛物线，

∴，解得：（舍去），．

②∵抛物线具有对称性，∴，

，OA=4，

．