��Ŀ����
����Ŀ������ģ�ͣ�
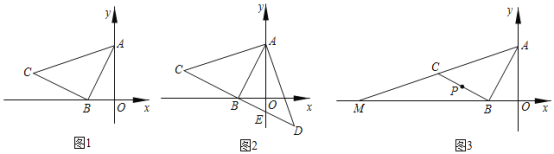
��������ͼ1��A��B��ֱ��![]() ͬ�Ե��������㣮
ͬ�Ե��������㣮

���⣺��ֱ��![]() ��ȷ��һ��P��ʹPA+PB��ֵ��С��
��ȷ��һ��P��ʹPA+PB��ֵ��С��
����������A����ֱ��![]() �ĶԳƵ�A��������A��B��
�ĶԳƵ�A��������A��B��![]() �ڵ�P����PA+PB=A��B��ֵ��С������֤������
�ڵ�P����PA+PB=A��B��ֵ��С������֤������
ģ��Ӧ�ã�
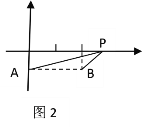
��1����ͼ2,��֪ƽ��ֱ������ϵ��������A��0��-1����B��2��-1��,PΪx����һ����, ��PA+PB��ֵ��Сʱ����P�ĺ�������______����ʱPA+PB����Сֵ��______��
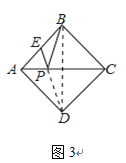
��2����ͼ3��������ABCD�ı߳�Ϊ2��EΪAB���е㣬P��AC��һ����.�������ζԳ��Կ�֪��B��D����ֱ��AC�Գƣ�����BD����PB+PE����Сֵ��______��
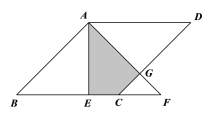
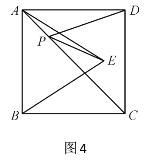
��3����ͼ4,������ABCD�����Ϊ12����ABE�ǵȱ������Σ���E��������ABCD�ڣ��ڶԽ���AC����һ����P����PD��PE����СֵΪ ��
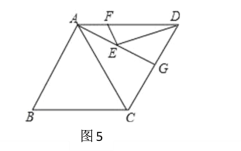
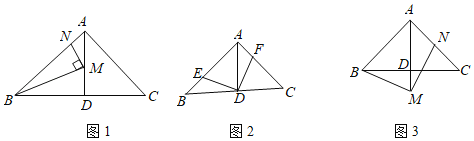
��4����ͼ5,������ABCD�У�AB=8����B=60������G�DZ�CD�ߵ��е㣬��E��F�ֱ���AG��AD�ϵ��������㣬��EF+ED����Сֵ��_______________.
���𰸡���1����P�ĺ������� 1 ����ʱPA+PB����Сֵ��![]() ����2��PB+PE����Сֵ��
����2��PB+PE����Сֵ��![]() ��3�������СֵΪ
��3�������СֵΪ ![]() ����4��EF+ED����Сֵ��
����4��EF+ED����Сֵ��![]()
��������
��1��ȡ��A����x��ԳƵĵ�A��������A��B����x����P����BH��x����H�����OP���õ���P�ĺ����꣬���ݹ��ɶ������A��B���õ��𰸣�
��2����������PB+PE=PD+PE=DE������ADE�У����ݹ��ɶ�����ü��ɣ�
��3�����ڵ�B��D����AC�Գƣ���������BD����AC�Ľ��㼴ΪF�㣮��ʱPD+PE=BE��С����BE�ǵȱ���ABE�ıߣ�BE=AB����������ABCD�����Ϊ12�������AB�ij����Ӷ��ó������
��4����DH��AC����ΪH��AG���ڵ�E����H����AG�ĶԳƵ�ΪF����ʱEF+ED��С=DH����֤����ADC�ǵȱ������Σ���RT��DCH�����ù��ɶ������ɽ�����⣮
��1��ȡ��A����x��ԳƵĵ�A��������A��B����x����P����BH��x����H��
���ʱPA+PB��ֵ��С��
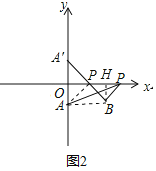
��OA��=OA=1��BH=1��BH��OA����
��OP=PH=1��
���P�������1��
PA+PB=A��B=![]() ��
��
�ʴ�Ϊ��1��2![]() ��
��
��2�����ı���ABCD�������Σ�
��AC��ֱƽ��BD��
��PB=PD��
�������ã�PB+PE=PD+PE=DE��
����ADE�У����ݹ��ɶ����ã�DE=![]() ��
��
��3������BD����AC���ڵ�F��

�ߵ�B��D����AC�Գƣ�
��PD=PB��
��PD+PE=PB+PE=BE����
��������ABCD�����Ϊ12��
��AB=2![]() ��
��
�֡ߡ�ABE�ǵȱ������Σ�
��BE=AB=2![]() ��
��
��������СֵΪ2![]() ��
��
��4����ͼ��DH��AC����ΪH��AG���ڵ�E��
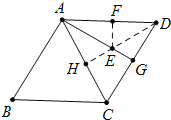
���ı���ABCD�����Σ�
��AB=AD=CD=BC=8��
�ߡ�B=60����
���ADC=��B=60����
���ADC�ǵȱ������Σ�
��AG�����ߣ�
���GAD=��GAC
���H����AG�ĶԳƵ�F��AD�ϣ���ʱEF+ED��С=DH��
��RT��DHC�У��ߡ�DHC=90����DC=6����CDH=![]() ��ADC=30����
��ADC=30����
��CH=![]() DC=4��DH=
DC=4��DH=![]() ��
��
��EF+DE����Сֵ=DH=4![]() ��
��