Question

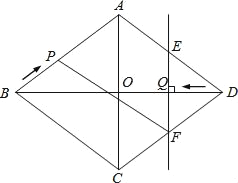
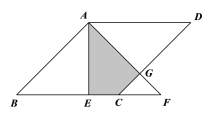
【题目】如图，在菱形ABCD中，AE⊥BC于E，将△ABE沿AE所在直线翻折得△AEF，若AB＝2，∠B＝45°，则△AEF与菱形ABCD重叠部分（阴影部分）的面积为（ ）.

A. 2 B. C. D.

Answer 1

【答案】D

【解析】

在边长为2的菱形ABCD中，∠B=45°，AE为BC边上的高，可求得AE的长，求得△ABF、△AEF、△CGF的面积，计算即可．

∵在边长为2的菱形ABCD中，∠B=45°，AE为BC边上的高，

∴AE=，

由折叠的性质可知，△ABF为等腰直角三角形，

∴S△ABF=ABAF=2，S△ABE=1，

∴CF=BF-BC=2-2，

∵AB∥CD，

∴∠GCF=∠B=45°，

又由折叠的性质知，∠F=∠B=45°，

∴CG=GF=2-．

∴S△CGF=GCGF=3-2，

∴重叠部分的面积为：2-1-（3-2）=2-2，

故选D．