��Ŀ����
����Ŀ�����Ķ����в��ϣ�
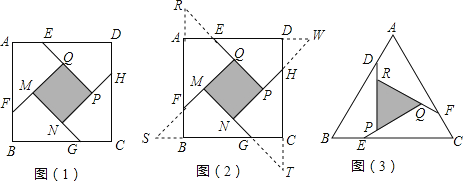
С����������һ�����⣺��ͼ1���ڱ߳�Ϊa(a��2)��������ABCD�����Ϸֱ��ȡAE=BF=CG=DH=1������AFQ=��BGM=��GHN=��DEP=45��ʱ����������MNPQ�������
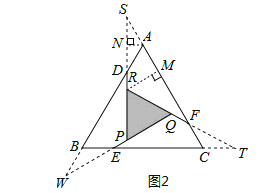
С�����֣��ֱ��ӳ�QE��MF��NG��PH��FA��GB��HC��ED���ӳ����ڵ�R��S��T��W���ɵ���RQF����SMG����TNH����WPE���ĸ�ȫ�ȵĵ���ֱ��������(��ͼ2) ��
��ش�
(1)���������ĸ�����ֱ��������ƴ��һ���µ�������(��϶���ص�)��������������εı�Ϊ ��
(2)��������MNPQ�������
(3)�ο�С��˼������ķ�����������⣺
��ͼ3���ڵȱ���ABC�����Ϸֱ��ȡAD=BE=CF���ٷֱ����D��E��F��BC��AC��AB�Ĵ��ߣ��õ��ȱ���RPQ����S��RPQ=![]() ����AD�ij���
����AD�ij���
���𰸡���1��a
��2���ߡ�RQF����SMG����TNH����WPE�ĸ�ȫ�ȵĵ���ֱ�������������Ϊ![]() ��������ABCD�����Ϊ
��������ABCD�����Ϊ![]() ����
����![]() ��
��
��3��![]()
�������������������1���ĸ�����ֱ�������ε�б�߳�Ϊa����ƴ�ɵ����������Ϊa2���߳�Ϊa��
��2������ͼ2��ʾ��������MNPQ����������ĸ�����С����ֱ�������ε����֮�ͣ��ݴ����������MNPQ�������
��3������С���Ľ���˼·����������ͬ���ĵȻ��任�����ͼ1��ʾ������������������RSF����QET����PDW������͵��ڵȱ���������ABC�����������Ӱ��������PQR����������������ߵ��������ε����֮�ͣ��ݴ��з������AD�ij��ȣ�
�����������1���ĸ�����ֱ�������ε�б�߳�Ϊa����б���ϵĸ�Ϊ![]() a��
a��
ÿ������ֱ�������ε����Ϊ�� ![]() a��
a��![]() a=
a=![]() a2��
a2��
��ƴ�ɵ������������Ϊ��4��![]() a2=a2������ԭ������ABCD�����ȣ�
a2=a2������ԭ������ABCD�����ȣ�
������������εı߳�Ϊa��
��2�����ĸ�����ֱ�������ε������Ϊa2��������ABCD�����Ϊa2��
��S������MNPQ=S��ARE+S��DWH+S��GCT+S��SBF=4S��ARE=4��![]() ��12=2��
��12=2��
��3����ͼ1��ʾ���ֱ��ӳ�RD��QF��PE����FA��EC��DB���ӳ����ڵ�S��T��W��
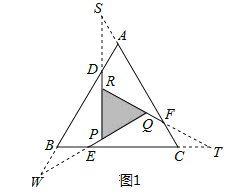
�������ã���RSF����QET����PDW��Ϊ����30���ĵ��������Σ���ױ߳���������ABC�ı߳���
������ȱ������α߳�Ϊa����SF=AC=a��
���ͼ2��ʾ������R��RM��SF�ڵ�M����MF=![]() SF=
SF=![]() a��
a��
��Rt��RMF��RM=MFtan30��=![]() a��
a��![]() =
=![]() a��
a��
��S��RSF=img src="http://thumb.zyjl.cn/questionBank/Upload/2017/12/28/23/c8f2bc24/SYS201712282307356414948798_DA/SYS201712282307356414948798_DA.018.png" width="16" height="41" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />a��![]() a=
a=![]() a2��
a2��
����A��AN��SD�ڵ�N����AD=AS=x��
��AN=ADsin30��=![]() x��SD=2ND=2ADcos30��=
x��SD=2ND=2ADcos30��=![]() x��
x��
��S��ADS=![]() SDAN=
SDAN=![]() ��
��![]() x��
x��![]() x=
x=![]() x2��
x2��
������������������RSF����QET����PDW�������=3S��RSF=3��![]() a2=
a2=![]() a2��
a2��
��S��RPQ=S��ADS+S��CFT+S��BEW=3S��ADS��
��![]() =3��
=3��![]() x2����x2=
x2����x2=![]() ��
��
���x=![]() ��x=-
��x=-![]() ���������⣬��ȥ��
���������⣬��ȥ��
��x=![]() ����AD�ij�Ϊ
����AD�ij�Ϊ![]() ��
��

 ���ɶ��ȫ���ƿؾ�ϵ�д�
���ɶ��ȫ���ƿؾ�ϵ�д�