Question

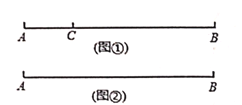
【题目】如图①，点C在线段AB上，图中共有三条线段AB、AC和BC，若其中有一条线段的长度是另外一条线段长度的2倍，则称点C是段AB的“2倍点”．

（1）线段的中点__________这条线段的“2倍点”；（填“是”或“不是”）

（2）若AB＝15cm，点C是线段AB的“2倍点”．求AC的长；

（3）如图②，已知AB＝20cm．动点P从点A出发，以2cm／s的速度沿AB向点B匀速移动．点Q从点B出发，以1cm/s的速度沿BA向点A匀速移动．点P、Q同时出发，当其中一点到达终点时，运动停止，设移动的时间为t（s），当t＝_____________s时，点Q恰好是线段AP的“2倍点”．（请直接写出各案）

Answer 1

【答案】（1）是；（2）5cm或7.5cm或10cm；（3）10或．

【解析】

（1）根据“2倍点”的定义即可求解；

（2）分点C在中点的左边，点C在中点，点C在中点的右边三种情况，进行讨论求解即可；

（3）根据题意画出图形，P应在Q的右边，分别表示出AQ、QP、PB，求出t的范围．然后根据（2）分三种情况讨论即可．

（1）∵整个线段的长是较短线段长度的2倍，∴线段的中点是这条线段的“2倍点”．

故答案为：是；

（2）∵AB＝15cm，点C是线段AB的2倍点，∴AC＝155cm或AC＝157.5cm或AC＝1510cm．

（3）∵点Q是线段AP的“2倍点”，∴点Q在线段AP上．如图所示：

由题意得：AP=2t，BQ=t，∴AQ=20-t，QP=2t-（20-t）=3t-20，PB=20-2t．

∵PB=20-2t≥0，∴t≤10．

∵QP=3t-20≥0，∴t≥，∴≤t≤10．

分三种情况讨论：

①当AQ＝AP时，20-t＝×2t，解得：t＝12＞10，舍去；

②当AQ＝AP时，20-t＝×2t，解得：t＝10；

③当AQ＝AP时，20-t＝×2t，解得：t；

答：t为10或时，点 Q是线段AP的“2倍点”．