题目内容
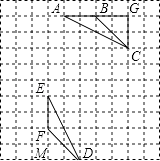
【题目】如图,在10×10的正方形网格中,△ABC的顶点和线段EF的端点都在边长为1的小正方形的顶点上. 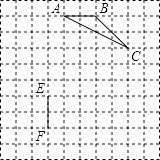
(1)填空:tanA= , AC=(结果保留根号);
(2)请你在图中找出一点D(仅一个点即可),连接DE、DF,使以D、E、F为顶点的三角形与△ABC全等,并加以证明.
【答案】
(1)![]() ;2
;2 ![]()
(2)解:图中找出一点D,连接DE、DF,△ABC≌△EFD,如右图所示,
证明:在Rt△EMD中,EM=4,MD=2,
根据勾股定理得:ED= ![]() =2
=2 ![]() ,
,
在Rt△FDM中,FM=2,MD=2,
根据勾股定理得:FD= ![]() =2
=2 ![]() ,
,
同理在Rt△BCG中,根据勾股定理得:BC=2 ![]() ,
,
在△ABC和△EFD中,
∵ 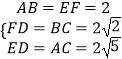 ,
,
∴△ABC≌△EFD(SSS).
【解析】(1)解:延长AB,过C作CG⊥AB,交延长线于点G, 在Rt△ACG中,CG=2,AG=4,
根据勾股定理得:AC= ![]() =2
=2 ![]() ,
,
tanA= ![]() ;
;
【考点精析】本题主要考查了勾股定理的概念和锐角三角函数的定义的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数才能正确解答此题.

【题目】为庆祝“六一”儿童节,某市中小学统一组织文艺汇演,甲、乙两所学校共92人(其中甲校的人数多于乙校的人数,且甲校的人数不足90人)准备统一购买服装参加演出;下面是某服装厂给出的演出服装的价格表
购买服装的套数 | 1套至45套 | 46套至90套 | 91套以上 |
每套服装的价格 | 60元 | 50元 | 40元 |
(1)如果两所学校分别单独购买服装一共应付5000元,甲、乙两所学校各有多少学生准备参加演出?
(2)如果甲校有10名同学抽调去参加书法绘画比赛不能参加演出,请你为两所学校设计一种最省钱的购买服装方案.