Question

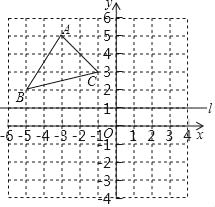
【题目】△ABC在直角坐标系中的位置如图所示，其中A（﹣3，5），B（﹣5，2），C（﹣1，3），直线l经过点（0，1），并且与x轴平行，△A′B′C′与△ABC关于线1对称．

（1）画出△A′B′C′，并写出△A′B′C′三个顶点的坐标：　 　；

（2）观察图中对应点坐标之间的关系，写出点P（a，b）关于直线l的对称点P′的坐标：　 　；

（3）若直线l′经过点（0，m），并且与x轴平行，根据上面研究的经验，写出点Q（c，d）关于直线1′的对称点Q′的坐标：　 　．

Answer 1

【答案】（1）A'（﹣3，﹣3），B'（﹣5，0），C'（﹣1，﹣1）；（2）（a，2﹣b）；（3）（c，2m﹣d）．

【解析】

（1）分别作出各点关于直线l的对称点，再顺次连接即可；

（2）根据（1）中各对应点坐标之间的关系即可得出结论；

（3）根据（2）中的结论推广即可．

（1）如图所示，△A′B′C′即为所求，A'（﹣3，﹣3），B'（﹣5，0），C'（﹣1，﹣1）；

故答案为：A'（﹣3，﹣3），B'（﹣5，0），C'（﹣1，﹣1）；

（2）由题可得：点P'的横坐标为a，设点P'的纵坐标为y，则=1，解得：y=2﹣b，∴点P（a，b）关于直线l的对称点P′的坐标为（a，2﹣b）．

故答案为：（a，2﹣b）；

（3）由题可得：点Q′的横坐标为c，设点Q'的纵坐标为y，则=m，解得：y=2m﹣d，∴点Q（c，d）关于直线1′的对称点Q′的坐标为（c，2m﹣d）．

故答案为：（c，2m﹣d）．