题目内容
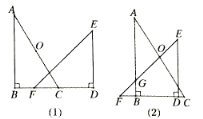
【题目】如图1,在∠A内部有一点P,连接BP、CP,请回答下列问题:

(1)求证:∠P=∠1+∠A+∠2;
(2)如图2,利用上面的结论,在五角星中,∠A+∠B+∠C+∠D+∠E= ;
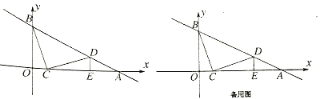
(3)如图3,如果在∠BAC间有两个向上突起的角,请你根据前面的结论猜想∠1、∠2、∠3、∠4、∠5、∠A之间有什么等量关系,直接写出结论即可.
【答案】(1)见解析;(2)180°;(3)∠4+∠5=∠1+∠2+∠3+∠A
【解析】
(1)连接AP并延长,再根据三角形内角与外角的性质即可求出∠BPC=∠1+∠A+∠2;
(2)先把五角星五个“角”归结到一个三角形中,再根据三角形内角和定理解答即可;
(3)分别连接AP、AD、AG并延长,再根据三角形外角的性质解答即可.
(1)连接AP并延长,如图:
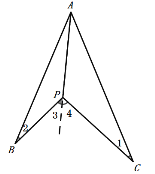
则∠3=∠2+∠BAP,∠4=∠1+∠PAC,
∴∠BPC=∠1+∠PAC+∠2+∠BAP =∠1+∠A+∠2;
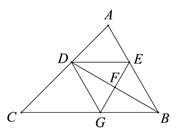
(2)如图:
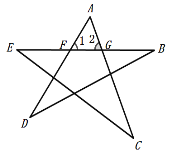
∵∠1是△DBF的外角,
∴∠1=∠B+∠D,
∵∠2是△ECG的外角,
∴∠2=∠C+∠E,
∵∠1、∠2、∠A是△AFG的内角,
∴∠1+∠2+∠A=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
(3) ∠4+∠5=∠1+∠2++∠3+∠A.理由如下:
作射线AP、AG,连结AD,如图,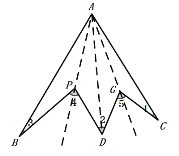
由(1)得∠4=∠3+∠BAD+∠ADP,∠5=∠ADG+∠1+∠DAC,
∴∠4+∠5=∠1+∠BAD+∠ADP+∠ADG+∠3+∠DAC=∠1+∠2+∠3+∠A.
故答案为:∠4+∠5=∠1+∠2+∠3+∠A.

练习册系列答案
相关题目