题目内容
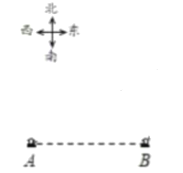
【题目】如图,A地和B地都是海上观测站,B地在A地正东方向,且A、B两地相距2海里. 从A地发现它的北偏东60°方向有一艘船C,同时,从B地发现船C在它的北偏东30°方向.
(1)在图中画出船C所在的位置;(要求用直尺与量角器作图,保留作图痕迹)
(2)已知三角形的内角和等于180°,求∠ACB的度数.
(3)此时船C与B地相距______海里.(只需写出结果,不需说明理由)
【答案】(1)见解析;(2)∠ACB=30°;(2)2.
【解析】
(1)根据方向角的概念,分别过A、B作射线,两条射线的交点即为船C的位置;
(2)首先求出∠CAB和∠ABC的度数,再根据三角形内角和是180°求出∠ACB的度数;
(3)由(2)中得出∠ACB=30°可知△ABC为等腰三角形,所以BC=AB.
(1)如图所示,C点即为船C所在的位置;

(2)在△ABC中,
∠CAB=90°-60°=30°,∠ABC=90°+30°=120°
∵∠ACB+∠CAB+∠ABC=180°
∴∠ACB=180°-30°-120°=30°
(3)∵∠ACB=∠CAB=30°
∴△ABC为等腰三角形
∴BC=AB=2海里
所以船C与B地相距2海里,
故答案为:2.

练习册系列答案
相关题目