题目内容
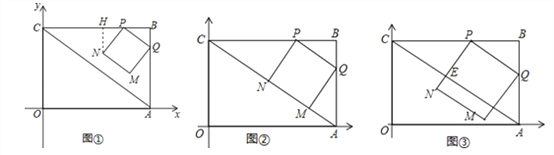
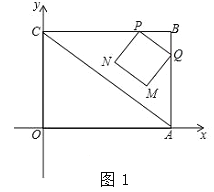
【题目】已知矩形OABC在如图所示平面直角坐标系中,点B的坐标为(4,3),连接AC.动点P从点B出发,以2cm/s的速度,沿直线BC方向运动,运动到C为止(不包括端点B、C),过点P作PQ∥AC交线段BA于点Q,以PQ为边向下作正方形PQMN,设正方形PQMN与△ABC重叠部分图形面积为S(cm2),设点P的运动时间为t(s).
(1)请用含t的代数式表示BQ长和N点的坐标;
(2)求S与t之间的函数关系式,并指出t的取值范围;
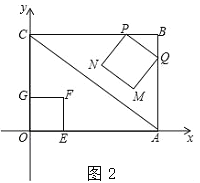
(3)如图2,点G在边OC上,且OG=1cm,在点P从点B出发的同时,另有一动点E从点O出发,以2cm/s的速度,沿x轴正方向运动,以OG、OE为一组邻边作矩形OEFG.试求当点F落在正方形PQMN的内部(不含边界)时t的取值范围.
【答案】(1)![]() ;(2)
;(2) ;(3)
;(3)![]()
【解析】试题分析:(1)作NH⊥BC于点H,根据△BPQ∽△BCA,利用相似三角形的对应边的比相等求得BQ,然后证明△BPQ≌△HNP,则BH以及HN的长即可利用t表示,则N的坐标即可求解;
(2)首先求出MN在AC上时t的值,然后分两种情况进行讨论,利用矩形的面积公式即可求解;
(3)求得AC的解析式,然后根据PQ∥AC,MN∥AC即可求得PQ和MN的解析式,F的坐标是(2t,1),把F的坐标分别代入PQ和MN的解析式即可求解
试题解析:解:(1)作NH⊥BC于点H.
∵PQ∥CA,∴△BPQ∽△BCA,∴![]() ,即
,即![]() ,解得:BQ=
,解得:BQ=![]() t.∵在△BPQ和△HNP,∴
t.∵在△BPQ和△HNP,∴ ,∴△BPQ≌△HNP,∴HP=BQ=
,∴△BPQ≌△HNP,∴HP=BQ=![]() t,NH=BP=2t,则BH=2t+
t,NH=BP=2t,则BH=2t+![]() t=
t=![]() t,则N点坐标(4﹣
t,则N点坐标(4﹣![]() t,3﹣2t);
t,3﹣2t);
(2)当MN在AC上时,如图②.
∵△BPQ∽△BCA,∴![]() ,即
,即![]() ,解得:PQ=
,解得:PQ=![]() t,当MN在AC上时,PN=PQ=
t,当MN在AC上时,PN=PQ=![]() t,△ABC∽△PNC,即
t,△ABC∽△PNC,即![]() ,即
,即![]() ,解得:t=
,解得:t=![]() .
.
则S=![]() t2.其中,0<t≤
t2.其中,0<t≤![]() .
.
当t>![]() 时,设PN交AC于点E,如图③.
时,设PN交AC于点E,如图③.
则△ABC∽△PEC,则![]() ,即
,即![]() ,解得:PE=
,解得:PE=![]() ,则S=﹣3t2+6t.其中,
,则S=﹣3t2+6t.其中,![]() <t<2.
<t<2.
综上所述:S= ;
;
(3)设AC的解析式是y=kx+b,则![]() ,解得:
,解得: ,则设直线MN的解析式是y=﹣
,则设直线MN的解析式是y=﹣![]() x+3,则﹣
x+3,则﹣![]() (4﹣
(4﹣![]() t)+c=3﹣2t,解得:c=6﹣
t)+c=3﹣2t,解得:c=6﹣![]() t,则直线的解析式是y=﹣
t,则直线的解析式是y=﹣![]() x+(6﹣
x+(6﹣![]() t).
t).
同理,直线PQ的解析式是y=﹣![]() x+(
x+(![]() ﹣
﹣![]() t),F的坐标是(2t,1).
t),F的坐标是(2t,1).
当点F落在MN上时,t=![]() .
.
当点F落在PQ上时,∴t=![]() <t<
<t<![]() .
.