题目内容
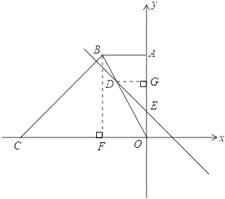
【题目】如图,在平面直角坐标系中,四边形OABC 的边OC 、OA 分别与 x 轴、 y 轴重合, AOC 90,BCO 45, AB // OC , BC 6 ![]() ,点C 的坐标为 9,0.
,点C 的坐标为 9,0.
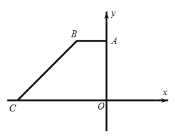

(1)求点 B 的坐标;
(2)若直线 DE 交四边形的对角线 BO 于点 D ,交 y 轴于点 E ,且OE 2 , OD 2BD ,求:
① ODE 的面积;
②点 D 的坐标.
(3)在(2)的条件下,坐标平面内是否存在点 P ,使以O 、E 、P 、D 为顶点的四边形是平行四边形? 若存在,请直接写出点 P 的坐标;若不存在,请说明理由.
【答案】(1)B(﹣3,6);(2)①S△ODE=2,②D(﹣2,4);(3)存在,P点坐标为(﹣2,6),(﹣2,2)或(2,﹣4).
【解析】
(1)过B点作BF⊥OC于点F,根据等腰直角三角形得到性质求得BF,CF的长即可得到B点坐标;
(2)过点D作DG⊥y轴于点G,根据相似三角形的性质可得DG与OG的长,即可得D点坐标,再利用三角形的面积公式求得△ODE的面积即可;
(3)分别以DE,OD,OE为对角线作平行四边形,分情况进行讨论即可.
(1)过点B作BF⊥x轴于F,
在Rt△BCF中,
∵∠BCO=45°,BC=6![]() ,
,
∴CF=BF=6,
∵C 的坐标为(﹣9,0),
∴AB=OF=3,
∴点B的坐标为(﹣3,6);
(2)过点D作DG⊥y轴于点G,
∵AB∥DG,
∴△ABO∽△GDO,
∴![]() ,
,
∵OD 2BD,AB=3,AO=6,
∴DG=2,OG=4,
∴S△ODE=![]() ,
,
点D坐标为:(﹣2,4);
(3)存在,如图2
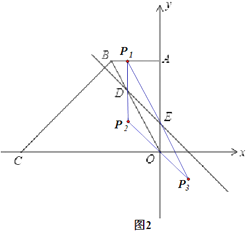
①平行四边形OEP1D,此时DE为对角线,
∴DP1∥OE,DP1=OE=2,
则P1(﹣2,6);
②平行四边形OEP2D,此时DO为对角线,
∴DP2∥OE,DP2=OE=2,
则P2(﹣2,2);
③平行四边形OEP3D,此时OE为对角线,
∴OP3∥DE,OP3=DE,
则P3(2,﹣4);
综上当P点坐标为(﹣2,6),(﹣2,2)或(2,﹣4)时,O、E、P、D为顶点的四边形是平行四边形.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案