��Ŀ����
����Ŀ���ҹ��Ŵ���ѧ������ֶ���λ������ǰ�У����С�������ǡ�����һ������ͼ����������εĹ��취�������ϵ�������1������ÿ������Ϊ���Ϸ���������֮�ͣ��������ˣ�a+b��n��nΪ����������չ��ʽ����a�Ĵ����ɴ�С��˳�����У���ϵ�����ɣ����磬���������е����е�������1��2��1��ǡ�ö�Ӧ��a+b��2=a2+2ab+b2չ��ʽ�е�ϵ���������е��ĸ���1��3��3��1��ǡ�ö�Ӧ�ţ�a+b��3=a3+3a2b+3ab2+b2չ��ʽ�е�ϵ���ȵȣ� 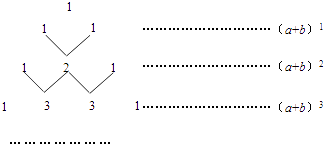
��1����������Ĺ��ɣ���a+b��5��չ��ʽ= ��
��2����������Ĺ��ɼ��㣺25��5��24+10��23��10��22+5��2��1= ��
���𰸡�
��1����a+b��5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
��2��1
���������⣺��1.���ߣ�a+b��1=a+b�� ��a+b��2=a2+2ab+b2 ��
��a+b��3=a3+3a2b+3ab2+b3 ��
��a+b��4=a4+4a3b+6a2b2+4ab3+b4 ��
�ࣨa+b��5=a5+5a4b+10a3b2+10a2b3+5ab4+b5 ��
���Դ��ǣ���a+b��5=a5+5a4b+10a3b2+10a2b3+5ab4+b5��
��2.��25��5��24+10��23��10��22+5��2��1=��2��1��5=15=1�����ݣ�a+b��5=a5+5a4b+10a3b2+10a2b3+5ab4+b5�������õó��ģ������Դ��ǣ�1��
�����㾫�����������⣬������Ҫ�˽���ȫƽ����ʽ(��ƽ����ĩƽ����������ĩ�����룮�͵�ƽ�����ټӣ��ȼ���Ӳ�ƽ��)��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��ij��ѧȥ��ͨ������Ʒ���ա���O�ʽ���������ƶ��ɽ���С�Сѧ����27������������һ����ѧ����ѧϰ������ҪxԪ������һ��Сѧ����ѧϰ������ҪyԪ�����꼶ѧ���O�ʽ���������ǡ�������С�Сѧ�������IJ���������±���
�꼶 | �O�ʽ����� | ����ƶ����ѧ | ����ƶ��Сѧ������������ |
���꼶 | 5000 | 2 | 5 |
���꼶 | 6000 | 3 | 5 |
���꼶 | 8000 |
��1����x��y��ֵ��
��2�����꼶ѧ���O���ʽ������������ƶ���С�Сѧ����ѧϰ���ã�������꼶ѧ��������ƶ���С�Сѧ��������