��Ŀ����
����Ŀ������������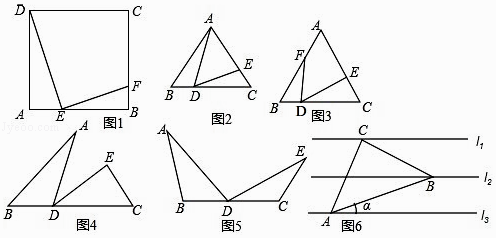
��1����ͼ1����֪E�Ǿ���ABCD�ı�AB��һ�㣬EF��DE��BC�ڵ�F��֤������ADE�ס�BFE��
��2��������ƵĻ���ͼ������ĸK�����Գ�Ϊ��K�������ƣ�������Ϊͼ�εĽṹ������һ��������3����ֱ��ϵ��Ҳ������Ϊ��һ������ֱ��������ͨ��3���Ƚ��ֻ������أ�
��ʽһ��ͼ2����֪�ȱ�������ABC����D��E�ֱ�ΪBC��AC�ϵĵ㣬��ADE=60�㣮
��ͼ������������������˵�����ɣ�
����ͼ3��������ADE�ڡ�ABC���ڲ�����ADE���߲���BC�غϣ����Ƶ�D��ʱ����תһ���ĽǶȣ�����������������
��3����ʽ����ͼ4�����ر�ʽ1ͼ���е��߶�AE���ڵõ�����ͼ���У�
�������B=��C=��ADE=50�㣬ͼ������������������˵�����ɣ�
����ͼ5������B=��C=��ADE=��a����aΪ����ǣ�����������������
��4����ʽ����֪����������ƽ��ֱ��ľ�����ȣ�������ֱ�ǡ�ABC����������ֱ���������ƽ��ֱ���ϣ���cosa��ֵ����ֱ��д���������
���𰸡�
��1��
�⣺���ı���ABCD�Ǿ��Σ�
���A=��B=90�㣬
���ADE+��AED=90�㣬
��EF��DE��
���AED+��BEF=90�㣬
���ADE=��BEF��
�ߡ�A=��B=90�㣬
���ADE�ס�BEF
��2��
�⣺�١ߡ�ABC�ǵȱ������Σ�
���B=��C=60�㣬
���������ε��ڽǺͶ����ã���ADB+��BAD=120�㣬
�ߡ�ADE=60�㣬
���ADB+��EDC=120�㣬
���BAD=��CDE��
�ߡ�B=��C=60�㣬
���ABD�ס�CDE
�ڡߡ�ABC�ǵȱ������Σ�
���B=��C=60�㣬
���������ε��ڽǺͶ����ã���FDB+��BFD=120�㣬
�ߡ�FDE=60�㣬
���FDB+��EDC=120�㣬
���BFD=��CDE��
�ߡ�B=��C=60�㣬
���FBD�ס�CDE��
��3��
�⣺�١�B=��C=50�㣬
���������ε��ڽǺͶ����ã���ADB+��BAD=130�㣬
�ߡ�ADE=50�㣬
���ADB+��EDC=130�㣬
���BAD=��CDE��
�ߡ�B=��C=130�㣬
���ABD�ס�CDE
��B=��C=�������������ε��ڽǺͶ����ã���ADB+��BAD=180�㩁����
�ߡ�ADE=����
���ADB+��EDC=180�㩁����
���BAD=��CDE��
�ߡ�B=��C=����
���ABD�ס�DCE��
��4��![]()
���������⣺��4������A��A��l1 �� ����B��BE��l1��l3��F��
���AFB=90�㣬
���CAD+��ACD=90�㣬
�ߡ�ACB=90�㣬
���ACD+��BCE=90�㣬
���CAD=��BCE��
�ڡ�ACD�͡�BCE�У� 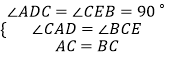 ��
��
���ACD�ա�BCE��
��AD=CE��CD=BE��
��ƽ����ľ���Ϊd��
��AD=CE=2d��BE=CD=d��
��DE=CD+CE=3d��
���ı���ADEF�Ǿ��Σ�
��AF=DE=3d��BF=d��
��Rt��ABF��AB= ![]() =
= ![]() d��
d��
��cos��= ![]() =
= ![]() =
= ![]() ��
��
�����㾫����������Ĺؼ������������������ε�Ӧ�õ����֪ʶ�����ղ�ߣ��������ܵ��ﶥ��������ĸ߶ȣ�ͨ���á���ͬһʱ�������Ӱ���ɱ�������ԭ���������ࣺ�������ܵ��������ľ�����������������������⣮

 ���ɶ��ȫ���ƿؾ�ϵ�д�
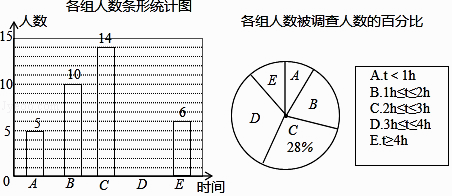
���ɶ��ȫ���ƿؾ�ϵ�д�����Ŀ���ס������˲μ�ѧУ��֯������ʵ��������ԣ����ڵ�5�β��Գɼ���ͼ��ʾ��

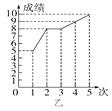
(1)�������ͼ�е�������д����
���� | ƽ���� | ���� | ���� |
�� | 8 | ||
�� | 8 | 2.8 |
(2)��ƽ�����ͷ������Ͽ���˭�ijɼ���Щ���ӷ�չ����������˭�ijɼ���Щ��