题目内容
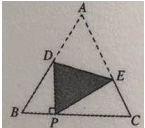
【题目】如图,把等边△ABC沿着DE折叠,使点A恰好落在BC边上的点P处,且DP⊥BC,若BP=4cm,则AD的长为（ ）
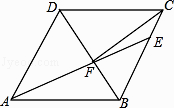
A. 5 B. 3 C. 4
D. 4
【答案】C
【解析】分析:根据等边三角形的性质可得∠B=60°,再根据DP⊥BC,可得∠BPD=90°,由三角形内角和性质可得∠BDP=30°,根据再30°的直角三角形中,30°所对直角边等于斜边的一半,可得BP=
,所以可得
,再根据勾股定理进行计算可求出DP= 4
,由翻折的性质可得AD=DP= 4.
详解: 因为△ABC是等边三角形,
所以∠B=60°,
因为DP⊥BC,
所以∠BPD=90°,
所以∠BDP=30°,
所以 BP=,
所以,
根据勾股定理可得:DP= 4,
由翻折的性质可得AD=DP= 4.
故选C.
练习册系列答案
相关题目
【题目】丰富的图形世界里有奇妙的数量关系，让我们通过下面这些几何体开始神奇的探索之旅．
观察：下面这些几何体都是简单几何体，请您仔细观察．
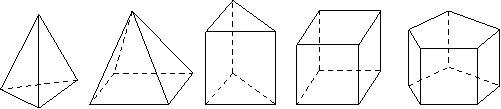
统计：每个几何体都会有棱（棱数为E）、面（面数为F）、顶点（顶点数为V），现将有关数据统计，完成下表．
几何体 | a | b | c | d | e |
棱数（E） | 6 | 9 | 15 | ||
面数（F） | 4 | 5 | 5 | 6 | |
顶点数（V） | 4 | 5 | 8 |
发现：（1）简单几何中，
；
（2）简单几何中，每条棱都是 个面的公共边；
（3）在正方体中，每个顶点处有 条棱，每条棱都有 个顶点，所以有2
3
．
应用：有一个叫“正十二面体”的简单几何体，它有十二个面，每个面都是正五边形，它的每个顶点处都有相同数目的棱．请问它有 条棱， 个顶点，每个顶点处有 条棱．
