题目内容
【题目】甲、乙两人参加学校组织的理化实验操作测试,近期的5次测试成绩如图所示.

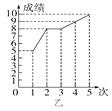
(1)请你根据图中的数据填写表格;
姓名 | 平均数 | 众数 | 方差 |
甲 | 8 | ||
乙 | 8 | 2.8 |
(2)从平均数和方差相结合看,谁的成绩好些?从发展趋势来看,谁的成绩好些?
【答案】(1)8 0.4 8;(2)从平均数和方差相结合看,甲的成绩好些;从发展趋势来看,乙的成绩好些.
【解析】(1)直接结合图中数据结合平均数以及方差求法分别得出答案;
(2)利用方差反映数据稳定性平均数是反映整体的平均水平进而分析得出答案.
(1)如图所示:乙的平均数为:![]()
S2甲=![]()
=0.4;
由图中数据可得:甲组数据的众数为8,
姓名 | 平均数 | 众数 | 方差 |
甲 | 8 | 8 | 0.4 |
乙 | 8 | 8 | 2.8 |
(2)从平均数和方差相结合看,甲的成绩好些;
从发展趋势来看,乙的成绩好些.

练习册系列答案
相关题目
【题目】从边长为a的大正方形纸板中挖去一个边长为b的小正方形后,将其裁成四个相同的等腰梯形(如图1),然后拼成一个平行四边形(如图2)。那么通过计算两个图形的阴影部分的面积,可以验证成立的公式是( )
A.a2-b2=(a-b)2 | B.(a+b)2="a+2ab+b" |
C.(a-b)2=a2-2ab+b2 | D.a2-b2=(a-b)(a+b) |

【题目】如图所示,将一张正方形纸片剪成四个大小一样的小正方形,然后将其中一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去。
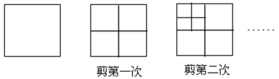
(1)完成下表:
剪的次数 | 1 | 2 | 3 | 4 | 5 | ... | n |
小正方形的个数 | 4 | 7 | 10 | ... |
|
(2)![]() .(用含n的代数式表示)
.(用含n的代数式表示)
(3)按上述方法,能否得到2018个小正方形?如果能,请求出n;如不能,请说明理由.