Question

【题目】如图1是某商场从一楼到二楼的自动扶梯，图2是侧面示意图，MN是二楼楼顶，MN∥PQ，点C在MN上，且位于自动扶梯顶端B点的正上方，BC⊥MN．测得AB＝10米，在自动扶梯底端A处测得点C的仰角为50°，点B的仰角为30°，求二楼的层高BC（结果保留根号）

（参考数据：sin50°＝0.77，cos50°＝0.64，tan50°＝1.20）

Answer 1

【答案】米

【解析】

延长CB交PQ于点D，在Rt△ADB中，求出BD，AD的长，然后在直角△CDA中利用三角函数即可求得CD的长，则BC即可得到．

解：延长CB交PQ于点D．

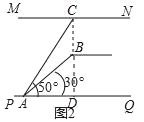
∵MN∥PQ，BC⊥MN，

∴BC⊥PQ．

在Rt△ABD中，∵AB＝10米，∠BAD＝30°，

∴（米），（米），

在Rt△CDA中，∠CDA＝90°，∠CAD＝50°，

∴（米），

∴（米）．