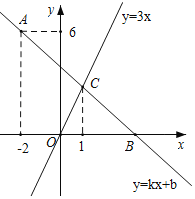��Ŀ����
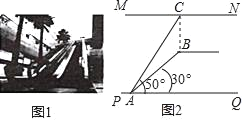
����Ŀ����֪��Rt��ABC�У���BAC��90�㣬CDΪ��ACB��ƽ���ߣ�����ACB��CD���ڵ�ֱ�߶��ۣ�ʹ��B���ڵ�B�䴦������AB'��BB'���ӳ�CD��BB'�ڵ�E�����ABC��2����0�㣼����45�㣩��

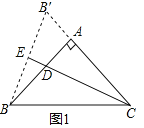
��1����ͼ1����AB��AC����֤��CD��2BE��
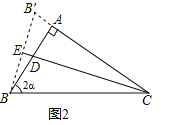
��2����ͼ2����AB��AC������CD��BE��������ϵ���ú�����ʽ�ӱ�ʾ����
��3����ͼ3������2���е��߶�BC�Ƶ�C��ʱ����ת�ǣ���+45�㣩���õ��߶�FC������EF��BC�ڵ�O������COE�����ΪS1����COF�����ΪS2����![]() ���ú�����ʽ�ӱ�ʾ����
���ú�����ʽ�ӱ�ʾ����
���𰸡���1��֤������������2��CD��2BEtan2������3��![]() sin��45�㩁������
sin��45�㩁������
��������
(1)�ɷ��ۿ�֪��BE��EB�䣬������ȫ�������ε�����֤��CD��BB�伴�ɣ�
(2) ��ͼ 2 �У� ���ۣ�CD��2BEtan2����ֻҪ֤����BAB��ס�CAD���ɵ�![]() ���Ƴ�
���Ƴ�![]() ���ɵ�CD��2BEtan2����
���ɵ�CD��2BEtan2����
(3) ����֤����ECF��90�㣬�ɡ�BEC+��ECF��180�㣬�Ƴ�BB���CF���Ƴ�![]() sin(45�㩁��)���ɴ˼��ɽ������.
sin(45�㩁��)���ɴ˼��ɽ������.
(1)��ͼ1�У�
��B��B�����EC�Գƣ�
��BB���EC��BE��EB�䣬
���DEB����DAC��90�㣬
�ߡ�EDB����ADC��
���DBE����ACD��
��AB��AC����BAB�䣽��DAC��90�㣬
���BAB���CAD��
��CD��BB�䣽2BE��
(2)��ͼ2�У����ۣ�CD��2BEtan2����
���ɣ���(1)��֪����ABB�䣽��ACD����BAB�䣽��CAD��90�㣬
���BAB��ס�CAD��
��![]() ��
��
��![]() ��
��
��CD��2BEtan2����
(3)��ͼ 3�У���Rt��ABC�У���ACB��90�㩁2����
��ECƽ�֡�ACB��
���ECB![]() (90�㩁2��)��45�㩁����
(90�㩁2��)��45�㩁����
�ߡ�BCF��45��+����
���ECF��45�㩁��+45��+����90�㣬
���BEC+��ECF��180�㣬
��BB���CF��
��![]() sin(45�㩁��)��
sin(45�㩁��)��
��![]() ��
��
��![]() sin(45�㩁��)��
sin(45�㩁��)��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
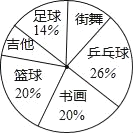
Сѧ��10����Ӧ����ϵ�д�����Ŀ��С��ij���ֻ������еĸ������ͳ�����������ͼ�����������ͼ����Ϣ������и��⣺
��Ŀ | �¹��ܷ� | �������� | ��;���� | ���ŷ� |
���/Ԫ | 5 | �� | �� | 25 |
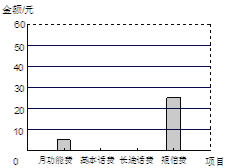
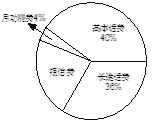
��1������С���ֻ����ѹ��ж���Ԫ��
��2������ͳ��ͼ�У���ʾ���ŷѵ����ε�Բ�Ľ�Ϊ���ٶȣ�
��3���뽫����������
��4���뽫����ͳ��ͼ����������
����Ŀ��ij�ӹ�����ÿ��3000Ԫ�ļ۸�50��ԭ�Ͻ��мӹ��������дּӹ���ÿ�ּӹ�����Ϊ600Ԫ����![]() �죬ÿ���ۼ�4000Ԫ�������о��ӹ���ÿ�ּӹ�����Ϊ900Ԫ����
�죬ÿ���ۼ�4000Ԫ�������о��ӹ���ÿ�ּӹ�����Ϊ900Ԫ����![]() �죬ÿ���ۼ�4500Ԫ���ֽ���50��ԭ��ȫ���ӹ��꣮�����дּӹ�x�֣�����yԪ��
�죬ÿ���ۼ�4500Ԫ���ֽ���50��ԭ��ȫ���ӹ��꣮�����дּӹ�x�֣�����yԪ��
��1������ɱ������y��x�ĺ�����ϵʽ����Ҫ��д�Ա����ķ�Χ����
��һ
�ּӹ�����/�� | 3 | 7 | x |
���ӹ�����/�� | 47 | �������� | �������� |
����
�ּӹ�����/�� | 3 | 7 | x |
�ּӹ�����/Ԫ | �������� | 2800 | �������� |
���ӹ�����/Ԫ | �������� | 25800 | �������� |
��2�����������20������ɣ���ΰ����������ܻ�����������������Ƕ��٣�