Question

【题目】在平面直角坐标系中，抛物线（m>0）与x轴交于A，B两点，点B在点A的右侧，顶点为C，抛物线与y轴交于点D，直线CA交y轴于E，且．

（1）求点A，点B的坐标；

（2）将△BCO绕点C逆时针旋转一定角度后，点B与点A重合，点O恰好落在y轴上，

①求直线CE的解析式；

②求抛物线的解析式．

Answer 1

【答案】（1） A（,0） B（,0）；(2) ①，②．

【解析】

（1）根据抛物线的解析式可得对称轴为x=2，利用得出CA:CE=3:4，由△AOE∽△AGC可得，进而求得OA、OB的长，即可求得点A、点B的坐标；

（2）根据旋转的性质求出C点坐标，利用C点坐标和△AOE∽△AGC可求得E点坐标，，分别利用待定系数法即可求得直线CE和抛物线的解析式．

解：（1）∵抛物线的解析式为，

∴对称轴为直线，

如图，设对称轴与x轴交于G，则轴，，

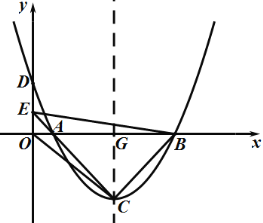
∴△AOE∽△AGC，

∴，

∵，

∴CA:CE=3:4 ，则，

∴，

∴，，

则，，

∴A(,0)， B(,0)；

（2）如图，设O旋转后落在点Q处，过点C作轴于点P，

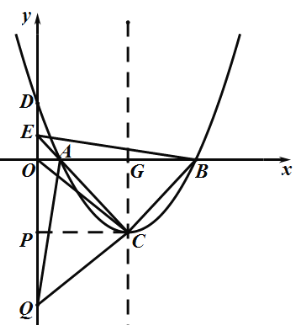
由旋转的性质得：△BCO≌△ACQ，

∴BO=AQ=，CO=CQ，

∴OQ=，

∵轴，

∴，

∴点C的坐标为，则

由（1）得△AOE∽△AGC，，

∴，即点E的坐标为，

①设CE的解析式为，分别代入C，E得：

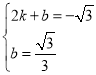，解得：，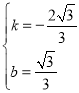

∴CE的解析式为；

②将A(,0)，C分别代入得：

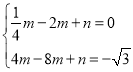，解得：，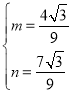

∴抛物线解析式为 ．