��Ŀ����
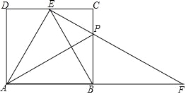
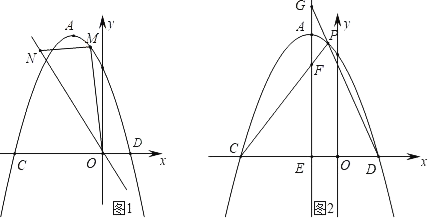
����Ŀ����ƽ��ֱ������ϵ�У���֪�����ߵĶ���ΪA����1��4�����Ҿ�����B����2��3������x��քe����C��D���㣨��C�ڵ�D����ࣩ��
��1����������߶�Ӧ�ĺ�������ʽ��
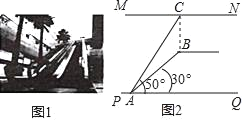
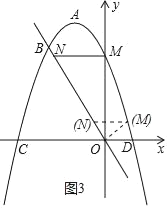
��2����ͼ1����M���������ϵ�һ�����㣬����ֱ��OB���Ϸ�������M��x���ƽ������ֱ��OB���ڵ�N������OM��
����MN�����ֵ��
�ڵ���OMNΪֱ��������ʱ��ֱ��д����M�����ꣻ
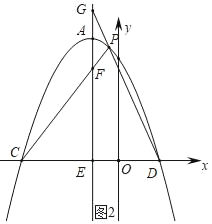
��3����ͼ2������A��ֱ�߽�x���ڵ�E����AE��y�ᣬ��P����������A��D֮���һ�����㣬ֱ��PC��PD��AE�քe����F��G���㣮����P�˶�ʱ��EF+EG�ĺ��Ƿ�Ϊ��ֵ�����ǣ�������ö�ֵ�������ǣ���˵�����ɣ�
���𰸡���1��y����x2��2x+3����2����![]() ���ڵ�M������Ϊ��0��3����
���ڵ�M������Ϊ��0��3����![]() ������3��EF+EG�ĺ�Ϊ��ֵ���ö�ֵΪ8�����ɼ�����
������3��EF+EG�ĺ�Ϊ��ֵ���ö�ֵΪ8�����ɼ�����
��������
��1���������ߵĶ���������������߶�Ӧ�ĺ�������ʽΪy��a��x+1��2+4�������B����������aֵ�������ɵó������߶�Ӧ�ĺ�������ʽ��
��2�����ɵ�B���������ô���ϵ�����ɵó�ֱ��OB�ĺ�������ʽ������ֱ��OB�������ߵĺ�������ʽ�ɷ����飬ͨ���ⷽ��������ֱ�ߺ������ߵĽ������꣬���M������Ϊ��m����m2��2m+3������2��m��![]() �������N������Ϊ��
�������N������Ϊ��![]() ����m2��2m+3���������ɵó�MN��
����m2��2m+3���������ɵó�MN��![]() �������ö��κ��������ʼ��ɽ����ֵ���⣻
�������ö��κ��������ʼ��ɽ����ֵ���⣻
����MN��x���֪��ONM��90�㣬�֡�OMN��90��͡�MON��90������������ǣ���i������OMN��90��ʱ���߶�OM��y���ϣ����ö��κ���ͼ���ϵ�������������������M�����ꣻ��ii������MON��90��ʱ��OM��OB���ɵ�B������ɵó�ֱ��OM���㣨3��2���������ɵó�ֱ��OM��Ӧ�ĺ�������ʽ������ֱ��OM�������ߵĺ�������ʽ�ɷ����飬ͨ���ⷽ����������M�����ꣻ
��3�����ö��κ���ͼ���ϵ�����������������C��D�����꣬���P������Ϊ��n����n2��2n+3������1��n��1�������ô���ϵ���������ֱ��CP��DP��Ӧ�ĺ�������ʽ���ɵ�A��������AE��y��ɵó�ֱ��AE��Ӧ�ĺ�������ʽ������һ�κ���ͼ���ϵ�����������������F��G�����꣬�����ɵó�EF��EG��EF+EG��ֵ��
��1���������ߵĶ���ΪA����1��4����
���������߶�Ӧ�ĺ�������ʽΪy��a��x+1��2+4��
��B����2��3������y��a��x+1��2+4���ã�3��a+4��
��ã�a����1��
�������߶�Ӧ�ĺ�������ʽΪy������x+1��2+4����y����x2��2x+3��
��2������ֱ��OB��Ӧ�ĺ�������ʽΪy��kx��k��0����
��B����2��3������y��kx���ã�3����2k��
��ã�k����![]() ��
��
��ֱ��OB��Ӧ�ĺ�������ʽΪy����![]() x��
x��
����ֱ��OB�������ߵĺ�������ʽ�ɷ����飬�ã�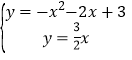 ��
��
��ã�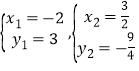 ��
��
���M��������m����m2��2m+3������2��m��![]() �������N��������
�������N��������![]() m2+
m2+![]() m��2����m2��2m+3����
m��2����m2��2m+3����
��MN��m����![]() m2+
m2+![]() m��2������
m��2������![]() m2��
m2��![]() m+2����
m+2����![]() ��m+
��m+![]() ��2+
��2+![]() ��
��
�ߩ�![]() ��0��
��0��
�൱m����![]() ʱ��MN������ֵΪ
ʱ��MN������ֵΪ![]() ��
��
�ڡ�MN��x�ᣬ
���ONM��90����
�������������ǣ���ͼ3��������
��i������OMN��90��ʱ���߶�OM��y���ϣ�
�ߵ�m��0ʱ��y����m2��2m+3��3��
���M��������0��3����
��ii������MON��90��ʱ��OM��OB��
�ߵ�B������Ϊ����2��3����
��㣨3��2����ֱ��OM�ϣ�
��ֱ��OM��Ӧ�ĺ�������ʽΪy��![]() x��
x��
����ֱ��OM�������ߵĺ�������ʽ�ɷ����飬�ã�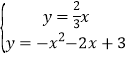 ��
��
��ã�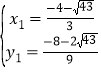 ���������⣬��ȥ����
���������⣬��ȥ����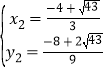 ��
��
���M��������![]() ����
����
������������M��������0��3����![]() ����
����
��3����y��0ʱ����x2��2x+3��0��
��ã�x1����3��x2��1��
���C����������3��0������D��������1��0����
���P��������n����n2��2n+3������1��n��1����
�ߵ�C������Ϊ����3��0������D������Ϊ��1��0����
��ֱ��CP��Ӧ�ĺ�������ʽΪy����1��n��x+3��3n��ֱ��DP��Ӧ�ĺ�������ʽΪy������n+3��x+n+3�������ô���ϵ�����������
�ߵ�A������Ϊ����1��4����AE��y�ᣬ
��ֱ��AE��Ӧ�ĺ�������ʽΪx����1��
��x����1ʱ��y����1��n��x+3��3n��2��2n��y������n+3��x+n+3��2n+6��
���F����������1��2��2n������G����������1��2n+6����
��EF��2��2n��EG��2n+6��
��EF+EG��8��
��EF+EG�ĺ�Ϊ��ֵ���ö�ֵΪ8��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д� Ŀ�����ϵ�д�
Ŀ�����ϵ�д�����Ŀ��С��ij���ֻ������еĸ������ͳ�����������ͼ�����������ͼ����Ϣ������и��⣺
��Ŀ | �¹��ܷ� | �������� | ��;���� | ���ŷ� |
���/Ԫ | 5 | �� | �� | 25 |
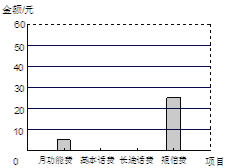
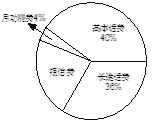
��1������С���ֻ����ѹ��ж���Ԫ��
��2������ͳ��ͼ�У���ʾ���ŷѵ����ε�Բ�Ľ�Ϊ���ٶȣ�
��3���뽫����������
��4���뽫����ͳ��ͼ����������