题目内容
如图,折叠矩形的一边AD,使得点D落在BC边上的点F处,已知AB=8cm, BC=10cm,则EC="_____________;" 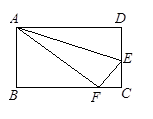

3
用勾股定理易得BF的长,也就求得了CF的长,进而根据△CEF是直角三角形利用勾股定理可得CE的长.
解:由折叠可得AD=AF=10cm,DE=EF,
又AB=8cm,
在Rt△ABF中,根据勾股定理得:BF=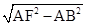 =6(cm),
=6(cm),
∴FC=BC-BF=10-6=4(cm),
∵CE2+CF2=EF2,
∴CE2+42=(8-CE)2,
解得CE=3cm,
解:由折叠可得AD=AF=10cm,DE=EF,
又AB=8cm,
在Rt△ABF中,根据勾股定理得:BF=
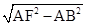 =6(cm),
=6(cm),∴FC=BC-BF=10-6=4(cm),
∵CE2+CF2=EF2,
∴CE2+42=(8-CE)2,
解得CE=3cm,

练习册系列答案
相关题目
 平分
平分 ;
; ,求
,求 的面积.
的面积.
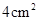 ,则梯形ABCD的面积为 cm2.
,则梯形ABCD的面积为 cm2.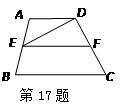
 被两条与边平行的线段
被两条与边平行的线段 分割成四个小矩形,
分割成四个小矩形, 与
与 交于点
交于点 .
.
 ,证明:
,证明: ;
; ,证明:
,证明: ;
; 的周长为1,求矩形
的周长为1,求矩形 的面积.
的面积. 中,
中, 平分
平分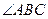 交
交 于点
于点 ,
, 平分
平分
 交
交 于点
于点 .
. ;
; ,则判断四边形
,则判断四边形 是什么特殊四边形,请证明你的结论.
是什么特殊四边形,请证明你的结论. 


 ,则菱形较短的对角线长是( )
,则菱形较短的对角线长是( )

 矩形ABCD中,点E在边AD上,EF⊥CE且与AB相交于点F,若DE=2,AD+DC=8,且CE=EF,求AE的长。
矩形ABCD中,点E在边AD上,EF⊥CE且与AB相交于点F,若DE=2,AD+DC=8,且CE=EF,求AE的长。