题目内容
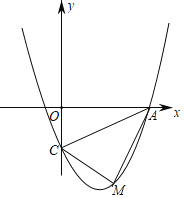
【题目】如图，抛物线经过点A(4，0)、B(﹣2，0)、C(0，﹣4)
(1)求抛物线的解析式；
(2)在抛物线AC段上是否存在点M，使△ACM的面积为3，求出在此时M的坐标，若不存在，说明理由.
【答案】(1)y＝
；(2)存在，M1(1，﹣
)，M2(3，﹣
).
【解析】
(1)设交点式为y＝a(x﹣4)(x+2)，然后把(0，﹣4)代入求出a即可；
(2)设M(a，
)，连接OM，则S△ACM＝S△OCM+S△OAM﹣S△OAC＝3，可得出关于a的方程，解方程即可求出点M的坐标.
解：(1)设抛物线解析式为：y＝a(x﹣4)(x+2)，
把(0，﹣4)代入得a×(﹣4)×2＝﹣4，解得a＝
，
∴抛物线解析式为：y＝；
(2)设M(a，)，连接OM，
∵S△ACM＝S△OCM+S△OAM﹣S△OAC＝3，
∴
﹣
＝3，
∴a2﹣4a+3＝0，
解得：a1＝3，a2＝1.
∴M1(1，﹣)，M2(3，﹣).
练习册系列答案
相关题目
